在數位成像領域,人們很容易認為解析度越高,畫質就越好。相機製造商通常以百萬像素數來推銷系統,而鏡頭製造商則強調解析度和清晰度。然而,實際上,影像品質不僅取決於鏡頭或感光元件的規格,還取決於它們的匹配程度。
奈奎斯特採樣正是為此而生。奈奎斯特標準最初源自於訊號處理原理,它為精準捕捉細節奠定了理論架構。在成像領域,它確保鏡頭的光學解析度與相機感測器的數位解析度和諧地協同工作。
本文從成像的角度解析了奈奎斯特取樣,解釋了光學和相機解析度之間的平衡,並為從攝影到科學成像等應用提供了實用指南。
什麼是奈奎斯特採樣?
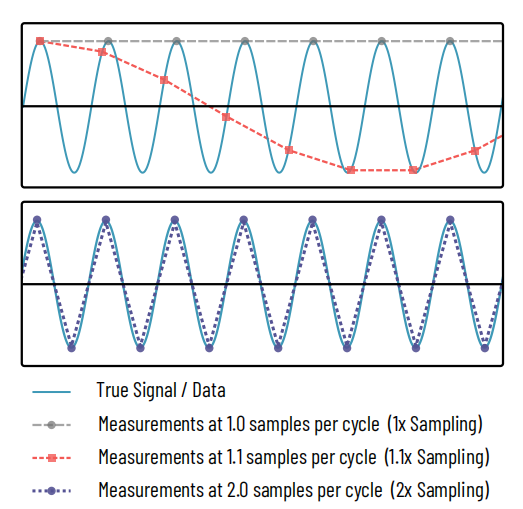
圖1:奈奎斯特取樣定理
頂部:在多個點測量或取樣正弦波訊號(青色)。灰色長虛線表示正弦訊號每個週期進行 1 次測量,僅捕獲訊號峰值,完全隱藏了訊號的真實本質。紅色細虛線表示每個樣本進行 1.1 次測量,顯示正弦波,但其頻率偏差。這類似於莫爾條紋。
底部:只有當每個週期採集 2 個樣本(紫色虛線)時,才會開始捕捉訊號的真實性質。
奈奎斯特取樣定理是電子、音訊處理、成像等領域訊號處理中常見的原理。該定理明確指出,要重建訊號中給定頻率,必須至少以該頻率的兩倍進行測量,如圖1所示。就光學解析度而言,這意味著物方像素尺寸最多只能是我們試圖捕捉的最小細節的一半,或者,就顯微鏡而言,最多是顯微鏡解析度的一半。
圖 2:奈奎斯特方形像素取樣:方向很重要
使用方形像素網格的相機,奈奎斯特定理中的 2 倍取樣率只能準確捕捉與像素網格完美對齊的細節。如果嘗試解析與像素網格成一定角度的結構,有效像素尺寸會更大,對角線方向最多可大 √2 倍。因此,取樣率必須是所需空間頻率的 2√2 倍,才能捕捉與像素網格成 45o 角的細節。
考慮圖2(上半部)可以清楚看出原因。假設像素大小設定為光學分辨率,兩個相鄰點源的峰值,或我們試圖解析的任何細節,每個峰值都有一個獨立的像素。雖然隨後分別檢測到這些峰值,但測量結果並沒有顯示它們是兩個獨立的峰值——這再次不符合我們對「解析」的定義。中間需要一個像素來捕捉訊號的波谷。這可以透過至少加倍空間取樣率來實現,即將物體空間像素大小減半。
光學解析度與相機解析度
為了理解奈奎斯特取樣在成像中的工作原理,我們需要區分兩種類型的解析度:
● 光學解析度:光學解析度由鏡頭決定,指的是其再現精細細節的能力。鏡頭品質、光圈和繞射等因素決定了這個極限。調製傳遞函數 (MTF) 通常用於衡量鏡頭在不同空間頻率下傳輸對比度的能力。
●相機解析度:相機解析度由感光元件決定,取決於像素大小、像素間距和整體感光元件尺寸。CMOS相機直接定義其奈奎斯特頻率,這決定了感測器可以捕捉的最大細節。
如果兩者不協調,就會出現問題。如果鏡頭的分辨率超過了感測器的分辨率,那麼它實際上就被「浪費」了,因為感測器無法捕捉到所有細節。相反,高解析度感光元件搭配低品質鏡頭,即使像素更高,影像品質也不會有任何提升。
如何平衡光學解析度和相機分辨率
平衡光學和感測器意味著將感測器的奈奎斯特頻率與鏡頭的光學截止頻率相匹配。
●相機感光元件的奈奎斯特頻率計算為 1 / (2 × 像素間距)。這定義了感測器在不產生混疊的情況下能夠取樣的最高空間頻率。
● 光學截止頻率取決於透鏡特性和繞射。
為了獲得最佳效果,感測器的奈奎斯特頻率應與鏡頭的分辨能力一致或略高於其分辨能力。實務上,一個好的經驗法則是確保像素間距約為鏡頭最小可分辨特徵尺寸的一半。
例如,如果鏡頭可以分辨出 4 微米的細節,那麼像素尺寸約為 2 微米的感光元件將很好地平衡系統。
奈奎斯特與相機解析度的匹配以及方形像素的挑戰
縮小物方像素尺寸的代價是光收集能力的下降。因此,平衡分辨率和光收集的需求至關重要。此外,較大的物方像素尺寸往往能夠提供更大的成像視野。對於需要精細解析度的應用,據說可以實現以下「經驗法則」的最佳平衡:物方像素尺寸乘以某個符合奈奎斯特定律的因子後,應等於光學解析度。這個量稱為相機解析度。
平衡光學元件和感測器通常歸結為確保相機的有效採樣解析度與鏡頭的光學解析度極限相符。當滿足以下條件時,系統即被稱為「匹配奈奎斯特」:
相機解析度=光學解析度
相機解析度由下式給出:
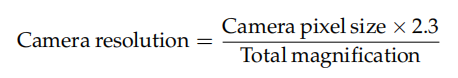
通常建議的考慮奈奎斯特的因子是 2.3,而不是 2。原因如下。
相機像素(通常)為正方形,排列在二維網格上。對邊公式中定義的像素大小表示像素沿該網格軸線的寬度。如果我們試圖解析的特徵相對於該網格呈除 90° 整數倍以外的任何角度,則有效像素大小將會更大,最高可達 √2 ≈ 45° 角像素大小的 1.41 倍。如圖 2(下半部)所示。
因此,根據奈奎斯特準則,所有方向的建議係數均為 2√2 ≈ 2.82。然而,由於前面提到的分辨率和光收集之間的權衡,根據經驗法則,建議取 2.3 作為折衷值。
奈奎斯特取樣在成像中的作用
奈奎斯特取樣是影像保真度的守門人。當取樣率低於奈奎斯特極限時:
● 欠採樣→ 導致混疊:錯誤細節、鋸齒狀邊緣或莫爾條紋。
● 過採樣→ 擷取的資料比光學元件所能傳送的資料更多,導致收益遞減:檔案更大、處理需求更高,而沒有明顯的改進。
正確的取樣確保影像清晰銳利,真實還原。它能夠在光學輸入和數位採集之間取得平衡,避免分辨率浪費或偽影的產生。
實際應用

●天文學:望遠鏡可以捕捉微弱而遙遠的訊號。感測器與望遠鏡光學系統相匹配,可確保獲得最清晰的細節,且不會產生偽影。
●攝影:高像素感光元件與無法解析同樣精細細節的鏡頭搭配,通常會導致清晰度的提升微乎其微。專業攝影師會平衡鏡頭和相機,以避免解析度的浪費。
●機器視覺和科學相機在品質控制和工業檢測中,由於採樣不足而失去微小特徵,可能導致缺陷部件無法檢測到。過採樣可能被刻意用於數位縮放或增強處理。
何時匹配奈奎斯特:過採樣和欠採樣
奈奎斯特採樣代表理想的平衡,但在實踐中,成像系統可能會根據應用故意過度採樣或欠採樣。
什麼是欠採樣
在靈敏度比解析最微小細節更重要的應用中,使用大於奈奎斯特要求的物方像素尺寸可以帶來顯著的光收集優勢。這被稱為欠採樣。
這會犧牲精細的細節,但在以下情況下可能會有優勢:
● 靈敏度至關重要:像素越大,收集的光就越多,從而提高低光成像的信噪比。
● 速度很重要:像素越少,讀出時間就越少,從而實現更快的擷取。
● 需要資料效率:在頻寬有限的系統中,檔案大小越小越好。
例如:在鈣或電壓成像中,訊號通常在感興趣的區域上取平均值,因此欠採樣可以改善光收集,而不會影響科學結果。
什麼是過採樣
相反,許多以解決精細細節為關鍵的應用,或使用採集後分析方法來恢復超出衍射極限的附加資訊的應用,需要比奈奎斯特要求更小的成像像素,這稱為過採樣。
雖然這不會提高真正的光學分辨率,但它可以帶來以下優勢:
● 實現數位變焦,且品質損失較少。
● 改進後處理(例如反捲積、去雜訊、超解析度)。
● 稍後對影像進行下取樣時減少可見的混疊。
例如:在顯微鏡中,高解析度 sCMOS 相機可能會對細胞結構進行過度取樣,以便計算演算法可以提取超出衍射極限的精細細節。
常見誤解
1.像素越高,影像就越清晰。
不對。清晰度取決於鏡頭的解析度以及感光元件的取樣是否合適。
2、任何好的鏡頭都可與任何高解析度感光元件配合良好。
鏡頭解析度和像素間距匹配不佳會限制效能。
3.奈奎斯特取樣僅與訊號處理有關,與成像無關。
相反,數位成像從根本上來說是一個取樣過程,奈奎斯特定律在這裡與音訊或通訊中一樣重要。
結論
奈奎斯特取樣不僅僅是一個數學抽象概念,它更是確保光學解析度和數位解析度協同工作的原理。透過協調鏡頭的解析度與感測器的取樣能力,成像系統能夠實現最高的清晰度,避免偽影或容量浪費。
對於顯微鏡、天文學、攝影和機器視覺等不同領域的專業人士來說,理解奈奎斯特取樣是設計或選擇能夠提供可靠結果的成像系統的關鍵。歸根究底,影像品質並非源自於將某項規格推向極致,而是源自於實現平衡。
常見問題解答
如果相機不滿足奈奎斯特採樣會發生什麼事?
當取樣率低於奈奎斯特極限時,感測器無法正確呈現精細細節,從而導致混疊,表現為鋸齒狀邊緣、莫爾條紋或真實場景中不存在的偽紋理。
像素大小如何影響奈奎斯特取樣?
像素越小,奈奎斯特頻率就越高,這意味著感測器理論上可以解析更精細的細節。但如果鏡頭無法達到這種分辨率,額外的像素就沒什麼價值,反而可能會增加雜訊。
奈奎斯特採樣對於單色感測器和彩色感測器是否不同?
是的。單色感測器的每個像素都直接取樣亮度,因此有效奈奎斯特頻率與像素間距相符。而採用拜耳濾鏡的彩色感測器,每個色彩通道都欠採樣,因此去馬賽克後的有效解析度會略低。
深圳市圖森光電技術有限公司 版權所有,轉載請註明出處:www.tucsen.com

 2004年9月25日
2004年9月25日