En la imatge digital, és fàcil suposar que una resolució més alta significa automàticament millors imatges. Els fabricants de càmeres sovint comercialitzen sistemes basats en el nombre de megapíxels, mentre que els fabricants d'objectius destaquen el poder de resolució i la nitidesa. Tot i això, a la pràctica, la qualitat de la imatge no només depèn de les especificacions de l'objectiu o del sensor individualment, sinó també de com de bé coincideixen.
Aquí és on entra en joc el mostreig de Nyquist. Originalment un principi del processament de senyals, el criteri de Nyquist estableix el marc teòric per capturar detalls amb precisió. En la imatge, garanteix que la resolució òptica proporcionada per una lent i la resolució digital del sensor d'una càmera funcionin conjuntament de manera harmoniosa.
Aquest article analitza el mostreig de Nyquist en el context de les imatges, explica l'equilibri entre la resolució òptica i la de la càmera i proporciona pautes pràctiques per a aplicacions que van des de la fotografia fins a les imatges científiques.
Què és el mostreig de Nyquist?
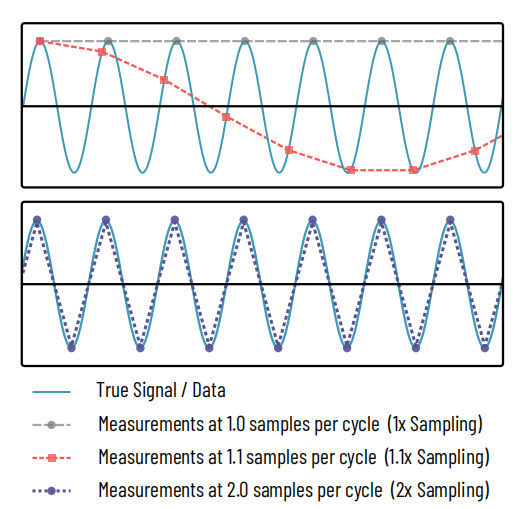
Figura 1: El teorema de mostreig de Nyquist
Part superior:Un senyal sinusoidal (cian) es mesura o es mostreja en múltiples punts. La línia grisa de punts llargs representa 1 mesura per cicle del senyal sinusoidal, capturant només els pics del senyal i amagant completament la veritable naturalesa del senyal. La corba vermella de punts finament discontinus captura 1,1 mesures per mostra, revelant una sinusoide però representant erròniament la seva freqüència. Això és anàleg a un patró de Moiré.
Part inferior:Només quan es prenen 2 mostres per cicle (línia puntejada lila) es comença a captar la veritable naturalesa del senyal.
El teorema de mostreig de Nyquist és un principi comú en el processament de senyals en electrònica, processament d'àudio, imatges i altres camps. El teorema deixa clar que per reconstruir una freqüència determinada en un senyal, s'han de fer mesures com a mínim el doble d'aquesta freqüència, tal com es mostra a la Figura 1. En el cas de la nostra resolució òptica, això significa que la mida de píxel de l'espai de l'objecte ha de ser com a màxim la meitat del detall més petit que intentem capturar o, en el cas d'un microscopi, la meitat de la resolució del microscopi.
Figura 2: Mostreig de Nyquist amb píxels quadrats: l'orientació importa
Si s'utilitza una càmera amb una graella de píxels quadrats, el factor de mostreig 2x del teorema de Nyquist només capturarà amb precisió els detalls que estiguin perfectament alineats amb la graella de píxels. Si s'intenta resoldre estructures en un angle respecte a la graella de píxels, la mida efectiva del píxel és més gran, fins a √2 vegades més gran a la diagonal. Per tant, la freqüència de mostreig ha de ser 2√2 vegades la freqüència espacial desitjada per capturar detalls a 45o respecte a la graella de píxels.
La raó d'això es fa evident considerant la Figura 2 (meitat superior). Imagineu-vos que la mida del píxel s'estableix a la resolució òptica, donant els pics de dues fonts puntuals veïnes, o qualsevol detall que intentem resoldre, cadascun amb el seu propi píxel. Tot i que aquests es detecten per separat, no hi ha cap indicació en els mesuraments resultants que siguin dos pics separats, i una vegada més no es compleix la nostra definició de "resolució". Es necessita un píxel entremig, capturant un punt baix del senyal. Això s'aconsegueix duplicant almenys la taxa de mostreig espacial, és a dir, reduint a la meitat la mida del píxel de l'espai de l'objecte.
Resolució òptica vs. resolució de la càmera
Per entendre com funciona el mostreig de Nyquist en la imatge, cal distingir entre dos tipus de resolució:
● Resolució òptica: Determinada per la lent, la resolució òptica fa referència a la seva capacitat per reproduir detalls fins. Factors com la qualitat de la lent, l'obertura i la difracció estableixen aquest límit. La funció de transferència de modulació (MTF) s'utilitza sovint per mesurar la capacitat d'una lent per transmetre el contrast a diferents freqüències espacials.
● Resolució de la càmera: Determinada pel sensor, la resolució de la càmera depèn de la mida del píxel, el pas entre píxels i les dimensions generals del sensor. El pas entre píxels d'unCàmera CMOSdefineix directament la seva freqüència de Nyquist, que determina el detall màxim que el sensor pot capturar.
Quan aquests dos no estan alineats, sorgeixen problemes. Una lent que supera el poder de resolució del sensor es "malgasta" de fet, ja que el sensor no pot capturar tots els detalls. Per contra, un sensor d'alta resolució combinat amb una lent de baixa qualitat dóna com a resultat imatges que no milloren malgrat tenir més megapíxels.
Com equilibrar la resolució òptica i la de la càmera
Equilibrar l'òptica i els sensors significa fer coincidir la freqüència de Nyquist del sensor amb la freqüència de tall òptic de la lent.
● La freqüència de Nyquist d'un sensor de càmera es calcula com a 1 / (2 × píxel pitch). Això defineix la freqüència espacial més alta que el sensor pot mostrejar sense aliasing.
● La freqüència de tall òptic depèn de les característiques de la lent i de la difracció.
Per obtenir els millors resultats, la freqüència de Nyquist del sensor ha d'alinear-se amb la capacitat de resolució de la lent o superar-la lleugerament. A la pràctica, una bona regla general és assegurar-se que el pas entre píxels sigui aproximadament la meitat de la mida de característica resoluble més petita de la lent.
Per exemple, si una lent pot resoldre detalls de fins a 4 micròmetres, un sensor amb mides de píxel de ~2 micròmetres equilibrarà bé el sistema.
Relacionant Nyquist amb la resolució de la càmera i el repte dels píxels quadrats
El compromís amb la disminució de la mida dels píxels de l'espai de l'objecte és la disminució de la capacitat de recollida de llum. Per tant, és important equilibrar la necessitat de resolució i la recollida de llum. A més, les mides de píxels de l'espai de l'objecte més grans tendeixen a transmetre un camp de visió més gran del subjecte de la imatge. Per a aplicacions que necessiten una resolució fina, es diu que s'aconsegueix un equilibri òptim "empirual" de la manera següent: la mida del píxel de l'espai de l'objecte, quan es multiplica per algun factor per tenir en compte el teorema de Nyquist, ha de ser igual a la resolució òptica. Aquesta quantitat s'anomena resolució de la càmera.
L'equilibri entre l'òptica i els sensors sovint es redueix a garantir que la resolució de mostreig efectiva de la càmera coincideixi amb el límit de resolució òptica de la lent. Es diu que un sistema "coincideix amb Nyquist" quan:
Resolució de la càmera = Resolució òptica
On la resolució de la càmera ve donada per:
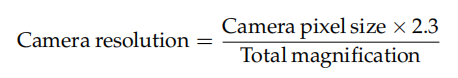
El factor per tenir en compte el coeficient de Nyquist que sovint es recomana és 2,3, no 2. La raó d'això és la següent.
Els píxels de la càmera són (normalment) quadrats i estan disposats en una quadrícula bidimensional. La mida del píxel, tal com es defineix per al seu ús a l'equació oposada, representa l'amplada dels píxels al llarg dels eixos d'aquesta quadrícula. Si les característiques que intentem resoldre es troben en qualsevol angle excepte un múltiple perfecte de 90° respecte a aquesta quadrícula, la mida efectiva del píxel serà més gran, fins a √2 ≈ 1,41 vegades la mida del píxel a 45°. Això es mostra a la Figura 2 (meitat inferior).
El factor recomanat segons el criteri de Nyquist en totes les orientacions seria, per tant, 2√2 ≈ 2,82. Tanmateix, a causa del compromís esmentat anteriorment entre la resolució i la recollida de llum, es recomana un valor de compromís de 2,3 com a regla general.
El paper del mostreig de Nyquist en la imatge
El mostreig de Nyquist és el guardià de la fidelitat de la imatge. Quan la taxa de mostreig cau per sota del límit de Nyquist:
● Submostreig → provoca àliesing: detalls falsos, vores dentades o patrons de moiré.
● Sobremostreig → captura més dades de les que pot oferir l'òptica, cosa que comporta rendiments decreixents: fitxers més grans i demandes de processament més elevades sense millores visibles.
Un mostreig correcte garanteix que les imatges siguin nítides i fidels a la realitat. Proporciona l'equilibri entre l'entrada òptica i la captura digital, evitant la resolució perduda en un costat o artefactes enganyosos en l'altre.
Aplicacions pràctiques
El mostreig de Nyquist no és només teoria, sinó que té aplicacions crítiques en totes les disciplines d'imatge:
● Microscòpia:Els investigadors han de triar sensors que mostregin almenys el doble del detall més petit resoluble per la lent de l'objectiu. Triar el correctecàmera de microscòpiaés crític, ja que la mida del píxel ha d'alinear-se amb la resolució limitada per difracció de l'objectiu del microscopi. Els laboratoris moderns sovint prefereixencàmeres sCMOS, que proporcionen un equilibri entre sensibilitat, rang dinàmic i estructures de píxels fines per a imatges biològiques d'alt rendiment.

● Fotografia:Combinar sensors d'alta resolució amb objectius que no poden resoldre detalls igualment fins sovint resulta en millores insignificants en la nitidesa. Els fotògrafs professionals equilibren els objectius i les càmeres per evitar malgastar resolució.
● Fotografia:Combinar sensors d'alta resolució amb objectius que no poden resoldre detalls igualment fins sovint resulta en millores insignificants en la nitidesa. Els fotògrafs professionals equilibren els objectius i les càmeres per evitar malgastar resolució.
● Visió artificial iCàmeres científiquesEn el control de qualitat i la inspecció industrial, la manca de petites característiques a causa d'un mostreig insuficient pot significar que les peces defectuoses passin desapercebudes. El sobremostreig es pot utilitzar deliberadament per al zoom digital o per al processament millorat.
Quan coincidir amb Nyquist: sobremostreig i inframostreig
El mostreig de Nyquist representa l'equilibri ideal, però a la pràctica, els sistemes d'imatge poden sobremostrejar o inframostrejar intencionadament segons l'aplicació.
Què és el submostreig?
En el cas d'aplicacions on la sensibilitat és més important que la resolució dels detalls més petits, l'ús d'una mida de píxel de l'espai de l'objecte que sigui més gran que les demandes de Nyquist pot comportar avantatges considerables en la recollida de llum. Això s'anomena submostreig.
Això sacrifica detalls fins, però pot ser avantatjós quan:
● La sensibilitat és fonamental: els píxels més grans recullen més llum, millorant la relació senyal-soroll en imatges amb poca llum.
● La velocitat és important: menys píxels redueixen el temps de lectura, cosa que permet una adquisició més ràpida.
● Cal eficiència en l'ús de les dades: en sistemes amb amplada de banda limitada, és preferible que els fitxers siguin més petits.
Exemple: En les imatges de calci o voltatge, els senyals sovint es calculen com a mitjana sobre les regions d'interès, de manera que el submostreig millora la recollida de llum sense comprometre el resultat científic.
Què és el sobremostreig?
Per contra, moltes aplicacions per a les quals la resolució de detalls fins és clau, o aplicacions que utilitzen mètodes d'anàlisi postadquisició per recuperar informació addicional més enllà del límit de difracció, requereixen píxels d'imatge més petits que els que exigeix Nyquist, el que s'anomena sobremostreig.
Tot i que això no augmenta la resolució òptica real, pot oferir avantatges:
● Activa el zoom digital amb menys pèrdua de qualitat.
● Millora el postprocessament (per exemple, deconvolució, eliminació de soroll, superresolució).
● Redueix l'aliasing visible quan les imatges es mostregen amb menys contrast més tard.
Exemple: En microscòpia, una càmera sCMOS d'alta resolució pot sobremostrejar estructures cel·lulars de manera que els algoritmes computacionals puguin extreure detalls fins més enllà del límit de difracció.
Idees errònies comunes
1. Més megapíxels sempre signifiquen imatges més nítides.
No és cert. La nitidesa depèn tant del poder de resolució de l'objectiu com de si el sensor mostreja correctament.
2. Qualsevol bon objectiu funciona bé amb qualsevol sensor d'alta resolució.
Una mala coincidència entre la resolució de la lent i el pas dels píxels limitarà el rendiment.
3. El mostreig de Nyquist només és rellevant en el processament de senyals, no en la imatge.
Al contrari, la imatge digital és fonamentalment un procés de mostreig, i Nyquist és tan rellevant aquí com en l'àudio o les comunicacions.
Conclusió
El mostreig de Nyquist és més que una abstracció matemàtica: és el principi que garanteix que la resolució òptica i digital funcionin conjuntament. En alinear el poder de resolució de les lents amb les capacitats de mostreig dels sensors, els sistemes d'imatge aconsegueixen la màxima claredat sense artefactes ni capacitat malgastada.
Per a professionals de camps tan diversos com la microscòpia, l'astronomia, la fotografia i la visió artificial, comprendre el mostreig de Nyquist és clau per dissenyar o triar sistemes d'imatge que ofereixin resultats fiables. En definitiva, la qualitat de la imatge no prové de portar una especificació a l'extrem, sinó d'aconseguir un equilibri.
Preguntes freqüents
Què passa si una càmera no compleix el mostreig de Nyquist?
Quan la freqüència de mostreig cau per sota del límit de Nyquist, el sensor no pot representar correctament els detalls fins. Això provoca un àliesing, que apareix com a vores dentades, patrons de moiré o textures falses que no existeixen a l'escena real.
Com afecta la mida del píxel al mostreig de Nyquist?
Els píxels més petits augmenten la freqüència de Nyquist, cosa que significa que el sensor teòricament pot resoldre detalls més fins. Però si la lent no pot oferir aquest nivell de resolució, els píxels addicionals afegeixen poc valor i poden augmentar el soroll.
El mostreig de Nyquist és diferent per a sensors monocroms i de color?
Sí. En un sensor monocrom, cada píxel mostra la luminància directament, de manera que la freqüència efectiva de Nyquist coincideix amb el pas del píxel. En un sensor de color amb un filtre Bayer, cada canal de color està inframostrejat, de manera que la resolució efectiva després del desmostratge és lleugerament inferior.
Tucsen Photonics Co., Ltd. Tots els drets reservats. Quan citeu, si us plau, indiqueu la font:www.tucsen.com

 25/09/04
25/09/04