25/09/04En la imagen digital, es fácil asumir que una mayor resolución se traduce automáticamente en mejores imágenes. Los fabricantes de cámaras suelen comercializar sistemas basados en la cantidad de megapíxeles, mientras que los fabricantes de objetivos destacan la capacidad de resolución y la nitidez. Sin embargo, en la práctica, la calidad de la imagen depende no solo de las especificaciones del objetivo o del sensor, sino también de su compatibilidad.
Aquí es donde entra en juego el muestreo de Nyquist. Originariamente un principio del procesamiento de señales, el criterio de Nyquist establece el marco teórico para capturar detalles con precisión. En el campo de la imagen, garantiza que la resolución óptica de un objetivo y la resolución digital del sensor de una cámara funcionen en armonía.
Este artículo analiza el muestreo de Nyquist en el contexto de la obtención de imágenes, explica el equilibrio entre la resolución óptica y la de la cámara y proporciona pautas prácticas para aplicaciones que van desde la fotografía hasta las imágenes científicas.
¿Qué es el muestreo de Nyquist?
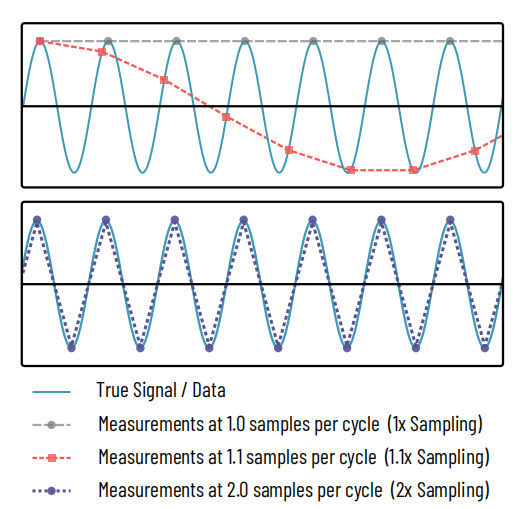
Figura 1: El teorema de muestreo de Nyquist
ArribaUna señal sinusoidal (cian) se mide o muestrea en múltiples puntos. La línea gris de trazos largos representa una medición por ciclo de la señal sinusoidal, capturando solo los picos de la señal y ocultando por completo su verdadera naturaleza. La curva roja de trazos finos captura 1,1 mediciones por muestra, revelando una sinusoide, pero distorsionando su frecuencia. Esto es análogo a un patrón de Moiré.
Abajo:Solo cuando se toman 2 muestras por ciclo (línea punteada violeta) se empieza a captar la verdadera naturaleza de la señal.
El teorema de muestreo de Nyquist es un principio común en el procesamiento de señales en electrónica, procesamiento de audio, imagen y otros campos. Este teorema establece que, para reconstruir una frecuencia dada en una señal, se deben realizar mediciones al menos al doble de esa frecuencia, como se muestra en la Figura 1. En el caso de nuestra resolución óptica, esto significa que el tamaño de píxel del espacio de objetos debe ser como máximo la mitad del detalle más pequeño que intentamos capturar o, en el caso de un microscopio, la mitad de su resolución.
Figura 2: Muestreo de Nyquist con píxeles cuadrados: la orientación importa
Al usar una cámara con una cuadrícula de píxeles cuadrados, el factor de muestreo 2x del teorema de Nyquist solo capturará con precisión los detalles perfectamente alineados con la cuadrícula. Si se intenta resolver estructuras en ángulo con respecto a la cuadrícula, el tamaño efectivo del píxel es mayor, hasta √2 veces mayor en la diagonal. Por lo tanto, la frecuencia de muestreo debe ser 2√2 veces la frecuencia espacial deseada para capturar detalles a 45° de la cuadrícula.
La razón de esto se hace evidente al considerar la Figura 2 (mitad superior). Imaginemos que el tamaño del píxel se ajusta a la resolución óptica, lo que otorga a los picos de dos fuentes puntuales vecinas, o a cualquier detalle que intentemos resolver, su propio píxel. Aunque estos se detectan por separado, las mediciones resultantes no indican que sean dos picos separados, y, una vez más, nuestra definición de "resolución" no se cumple. Se necesita un píxel intermedio que capture un valle de la señal. Esto se logra duplicando al menos la frecuencia de muestreo espacial, es decir, reduciendo a la mitad el tamaño del píxel en el espacio del objeto.
Resolución óptica vs. resolución de la cámara
Para entender cómo funciona el muestreo de Nyquist en imágenes, necesitamos distinguir entre dos tipos de resolución:
Resolución óptica: Determinada por la lente, la resolución óptica se refiere a su capacidad para reproducir detalles finos. Factores como la calidad de la lente, la apertura y la difracción determinan este límite. La función de transferencia de modulación (MTF) se utiliza a menudo para medir la eficacia de la transmisión del contraste de una lente a diferentes frecuencias espaciales.
● Resolución de la cámara: Determinada por el sensor, la resolución de la cámara depende del tamaño del píxel, la distancia entre píxeles y las dimensiones generales del sensor. La distancia entre píxeles de unacámara CMOSdefine directamente su frecuencia Nyquist, que determina el máximo detalle que el sensor puede capturar.
Cuando estos dos no están alineados, surgen problemas. Un objetivo que excede la capacidad de resolución del sensor se desperdicia, ya que este no puede capturar todos los detalles. Por el contrario, un sensor de alta resolución combinado con un objetivo de baja calidad produce imágenes que no mejoran a pesar de tener más megapíxeles.
Cómo equilibrar la resolución óptica y de la cámara
Equilibrar la óptica y los sensores significa hacer coincidir la frecuencia de Nyquist del sensor con la frecuencia de corte óptico de la lente.
La frecuencia de Nyquist de un sensor de cámara se calcula como 1 / (2 × paso de píxel). Esto define la frecuencia espacial más alta que el sensor puede muestrear sin aliasing.
● La frecuencia de corte óptico depende de las características de la lente y de la difracción.
Para obtener los mejores resultados, la frecuencia de Nyquist del sensor debe coincidir con la capacidad de resolución del objetivo o superarla ligeramente. En la práctica, una buena regla general es asegurar que la distancia entre píxeles sea aproximadamente la mitad del tamaño mínimo resoluble del objetivo.
Por ejemplo, si una lente puede resolver detalles de hasta 4 micrómetros, entonces un sensor con tamaños de píxeles de ~2 micrómetros equilibrará bien el sistema.
La compatibilidad de Nyquist con la resolución de la cámara y el desafío de los píxeles cuadrados
La desventaja de reducir el tamaño de píxel en el espacio del objeto es una menor capacidad de captación de luz. Por lo tanto, es importante equilibrar la necesidad de resolución y la de captación de luz. Además, los píxeles de mayor tamaño en el espacio del objeto tienden a ofrecer un campo de visión más amplio del sujeto que se captura. Para aplicaciones que requieren una resolución fina, se considera que el equilibrio óptimo se logra de la siguiente manera: el tamaño de píxel en el espacio del objeto, al multiplicarse por un factor que tenga en cuenta la ley de Nyquist, debe ser igual a la resolución óptica. Esta cantidad se denomina resolución de la cámara.
Equilibrar la óptica y los sensores suele implicar garantizar que la resolución de muestreo efectiva de la cámara coincida con el límite de resolución óptica del objetivo. Se dice que un sistema es "compatible con Nyquist" cuando:
Resolución de la cámara = Resolución óptica
Donde la resolución de la cámara viene dada por:
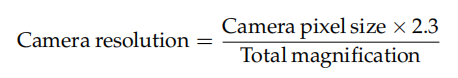
El factor a tener en cuenta para Nyquist que a menudo se recomienda es 2,3, no 2. La razón de esto es la siguiente.
Los píxeles de la cámara son (normalmente) cuadrados y están dispuestos en una cuadrícula bidimensional. El tamaño de píxel, tal como se define en la ecuación opuesta, representa el ancho de los píxeles a lo largo de los ejes de esta cuadrícula. Si las características que intentamos resolver se encuentran en cualquier ángulo que no sea un múltiplo perfecto de 90° con respecto a esta cuadrícula, el tamaño de píxel efectivo será mayor, hasta √2 ≈ 1,41 veces el tamaño de píxel a 45°. Esto se muestra en la Figura 2 (mitad inferior).
Por lo tanto, el factor recomendado según el criterio de Nyquist en todas las orientaciones sería 2√2 ≈ 2,82. Sin embargo, debido al equilibrio mencionado previamente entre la resolución y la captación de luz, se recomienda un valor de compromiso de 2,3 como regla general.
El papel del muestreo de Nyquist en la obtención de imágenes
El muestreo de Nyquist es el factor clave para la fidelidad de la imagen. Cuando la frecuencia de muestreo cae por debajo del límite de Nyquist:
● Submuestreo→ provoca aliasing: detalles falsos, bordes irregulares o patrones muaré.
● Sobremuestreo→ captura más datos de los que la óptica puede proporcionar, lo que genera rendimientos decrecientes: archivos más grandes y mayores demandas de procesamiento sin mejoras visibles.
Un muestreo correcto garantiza imágenes nítidas y fieles a la realidad. Proporciona el equilibrio entre la entrada óptica y la captura digital, evitando el desperdicio de resolución por un lado o artefactos engañosos por el otro.
Aplicaciones prácticas
El muestreo de Nyquist no es solo teoría: tiene aplicaciones críticas en todas las disciplinas de imágenes:
●MicroscopíaLos investigadores deben elegir sensores que muestren al menos el doble del detalle más pequeño que puede resolver el objetivo. Elegir el sensor adecuadocámara de microscopíaes fundamental, ya que el tamaño del píxel debe estar alineado con la resolución limitada por difracción del objetivo del microscopio. Los laboratorios modernos a menudo prefierencámaras sCMOS, que proporcionan un equilibrio de sensibilidad, rango dinámico y estructuras de píxeles finos para imágenes biológicas de alto rendimiento.
●AstronomíaLos telescopios captan señales tenues y distantes. La compatibilidad de los sensores con la óptica del telescopio garantiza el máximo detalle sin introducir artefactos.
●FotografíaLa combinación de sensores de alta resolución con objetivos que no pueden captar detalles con la misma precisión suele resultar en mejoras insignificantes en la nitidez. Los fotógrafos profesionales equilibran los objetivos y las cámaras para evitar el desperdicio de resolución.
●Visión artificial yCámaras científicasEn el control de calidad y la inspección industrial, la omisión de pequeñas características debido al submuestreo podría impedir la detección de piezas defectuosas. El sobremuestreo puede utilizarse deliberadamente para ampliar la imagen digital o mejorar el procesamiento.
Cuándo igualar Nyquist: sobremuestreo y submuestreo
El muestreo de Nyquist representa el equilibrio ideal, pero en la práctica, los sistemas de imágenes pueden muestrear en exceso o en defecto intencionalmente según la aplicación.
¿Qué es el submuestreo?
En aplicaciones donde la sensibilidad es más importante que la resolución de los detalles más minúsculos, usar un tamaño de píxel en el espacio de objetos mayor que el requerido por Nyquist puede generar ventajas considerables en la captura de luz. Esto se denomina submuestreo.
Esto sacrifica los detalles finos, pero puede ser ventajoso cuando:
● La sensibilidad es fundamental: los píxeles más grandes recogen más luz, lo que mejora la relación señal-ruido en imágenes con poca luz.
● La velocidad importa: menos píxeles reducen el tiempo de lectura, lo que permite una adquisición más rápida.
● Se requiere eficiencia de datos: es preferible utilizar archivos de menor tamaño en sistemas con ancho de banda limitado.
Ejemplo: en las imágenes de calcio o voltaje, las señales a menudo se promedian en las regiones de interés, por lo que el submuestreo mejora la recolección de luz sin comprometer el resultado científico.
¿Qué es el sobremuestreo?
Por el contrario, muchas aplicaciones para las que la resolución de detalles finos es clave, o aplicaciones que utilizan métodos de análisis posteriores a la adquisición para recuperar información adicional más allá del límite de difracción, requieren píxeles de imágenes más pequeños que los que exige Nyquist, lo que se denomina sobremuestreo.
Si bien esto no aumenta la resolución óptica real, puede brindar ventajas:
● Permite el zoom digital con menor pérdida de calidad.
● Mejora el posprocesamiento (por ejemplo, deconvolución, eliminación de ruido, superresolución).
● Reduce el aliasing visible cuando las imágenes se reducen posteriormente.
Ejemplo: en microscopía, una cámara sCMOS de alta resolución puede sobremuestrear estructuras celulares para que los algoritmos computacionales puedan extraer detalles finos más allá del límite de difracción.
Conceptos erróneos comunes
1、Más megapíxeles siempre significan imágenes más nítidas.
No es cierto. La nitidez depende tanto del poder de resolución del objetivo como del muestreo adecuado del sensor.
2、Cualquier buena lente funciona bien con cualquier sensor de alta resolución.
Una mala coincidencia entre la resolución de la lente y el paso de píxeles limitará el rendimiento.
3. El muestreo de Nyquist solo es relevante en el procesamiento de señales, no en la obtención de imágenes.
Por el contrario, la imagen digital es fundamentalmente un proceso de muestreo, y Nyquist es tan relevante aquí como en el audio o las comunicaciones.
Conclusión
El muestreo de Nyquist es más que una abstracción matemática: es el principio que garantiza la integración de la resolución óptica y digital. Al alinear el poder de resolución de las lentes con la capacidad de muestreo de los sensores, los sistemas de imagen logran la máxima claridad sin artefactos ni desperdicio de capacidad.
Para profesionales de campos tan diversos como la microscopía, la astronomía, la fotografía y la visión artificial, comprender el muestreo de Nyquist es clave para diseñar o elegir sistemas de imagen que ofrezcan resultados fiables. En definitiva, la calidad de la imagen no se basa en llevar una especificación al extremo, sino en lograr un equilibrio.
Preguntas frecuentes
¿Qué sucede si el muestreo de Nyquist no es satisfactorio en una cámara?
Cuando la frecuencia de muestreo cae por debajo del límite de Nyquist, el sensor no puede representar correctamente los detalles finos. Esto produce aliasing, que se manifiesta como bordes irregulares, patrones muaré o texturas falsas que no existen en la escena real.
¿Cómo afecta el tamaño del píxel al muestreo de Nyquist?
Los píxeles más pequeños aumentan la frecuencia de Nyquist, lo que significa que, en teoría, el sensor puede captar detalles más finos. Sin embargo, si el objetivo no puede ofrecer ese nivel de resolución, los píxeles adicionales aportan poco valor y pueden aumentar el ruido.
¿El muestreo de Nyquist es diferente para los sensores monocromáticos y de color?
Sí. En un sensor monocromático, cada píxel muestrea la luminancia directamente, por lo que la frecuencia de Nyquist efectiva coincide con la distancia entre píxeles. En un sensor de color con filtro Bayer, cada canal de color se submuestrea, por lo que la resolución efectiva tras el demosaico es ligeramente inferior.
Tucsen Photonics Co., Ltd. Todos los derechos reservados. Al citar, por favor, cite la fuente.www.tucsen.com
