Comprendre l'échantillonnage de Nyquist : équilibre entre la résolution optique et la résolution de la caméra |

En imagerie numérique, on a tendance à penser qu'une résolution plus élevée est synonyme de meilleures images. Les fabricants d'appareils photo commercialisent souvent des systèmes basés sur le nombre de mégapixels, tandis que les fabricants d'objectifs mettent en avant le pouvoir de résolution et la netteté. Pourtant, en pratique, la qualité d'image dépend non seulement des spécifications de l'objectif ou du capteur, mais aussi de leur adéquation.

C'est là qu'intervient l'échantillonnage de Nyquist. Principe issu à l'origine du traitement du signal, le critère de Nyquist établit le cadre théorique permettant de capturer avec précision les détails. En imagerie, il garantit l'harmonie entre la résolution optique d'un objectif et la résolution numérique du capteur d'un appareil photo.

Cet article décompose l'échantillonnage de Nyquist dans le contexte de l'imagerie, explique l'équilibre entre la résolution optique et celle de la caméra et fournit des directives pratiques pour des applications allant de la photographie à l'imagerie scientifique.

Qu'est-ce que l'échantillonnage de Nyquist ?

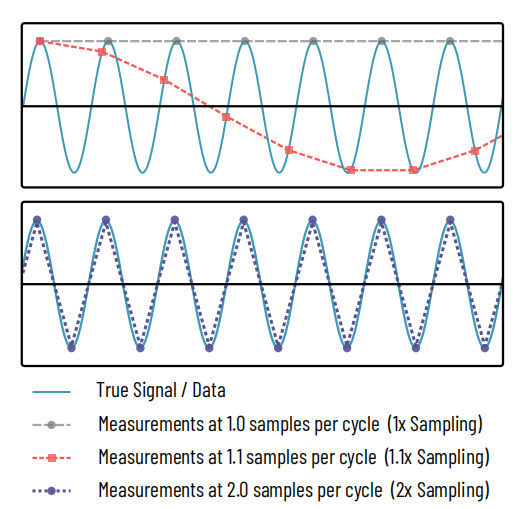
Figure 1 : Le théorème d'échantillonnage de Nyquist

HautUn signal sinusoïdal (cyan) est mesuré, ou échantillonné, en plusieurs points. La ligne grise en pointillés longs représente une mesure par cycle du signal sinusoïdal, capturant uniquement les pics du signal et masquant ainsi complètement sa véritable nature. La courbe rouge en pointillés fins capture 1,1 mesure par échantillon, révélant une sinusoïde mais dénaturant sa fréquence. Ceci est analogue à un effet de moiré.

Bas:Ce n'est que lorsque 2 échantillons sont prélevés par cycle (ligne pointillée violette) que la véritable nature du signal commence à être capturée.

Le théorème d'échantillonnage de Nyquist est un principe commun au traitement du signal en électronique, en traitement audio, en imagerie et dans d'autres domaines. Ce théorème précise que pour reconstituer une fréquence donnée dans un signal, des mesures doivent être effectuées à au moins deux fois cette fréquence, comme illustré à la figure 1. Dans le cas de notre résolution optique, cela signifie que la taille des pixels de notre espace objet doit être au plus égale à la moitié du plus petit détail que nous cherchons à capturer, ou, dans le cas d'un microscope, à la moitié de sa résolution.

Échantillonnage de Nyquist avec pixels carrés

Figure 2 : Échantillonnage de Nyquist avec des pixels carrés : l'orientation est importante

En utilisant une caméra dotée d'une grille de pixels carrés, le facteur d'échantillonnage 2x du théorème de Nyquist ne capturera avec précision que les détails parfaitement alignés sur la grille. Si l'on tente de résoudre des structures inclinées par rapport à la grille, la taille effective des pixels est plus grande, jusqu'à √2 fois plus grande en diagonale. Le taux d'échantillonnage doit donc être 2√2 fois supérieur à la fréquence spatiale souhaitée pour capturer les détails à 45° de la grille.

La raison en est évidente à la lecture de la figure 2 (partie supérieure). Imaginons que la taille des pixels soit définie sur la résolution optique, attribuant à chaque pic de deux sources ponctuelles voisines, ou de tout détail à résoudre, un pixel distinct. Bien que ces pics soient ensuite détectés séparément, les mesures obtenues n'indiquent pas qu'il s'agit de deux pics distincts ; une fois encore, notre définition de la « résolution » n'est pas respectée. Un pixel intermédiaire est nécessaire pour capturer un creux du signal. Ceci est obtenu en doublant au moins le taux d'échantillonnage spatial, c'est-à-dire en divisant par deux la taille des pixels de l'espace objet.

Résolution optique vs. résolution de l'appareil photo

Pour comprendre comment fonctionne l'échantillonnage de Nyquist en imagerie, nous devons distinguer deux types de résolution :

● Résolution optique : Déterminée par l'objectif, la résolution optique fait référence à sa capacité à reproduire les détails les plus fins. Des facteurs tels que la qualité de l'objectif, l'ouverture et la diffraction fixent cette limite. La fonction de transfert de modulation (FTM) est souvent utilisée pour mesurer la qualité de transmission du contraste par un objectif à différentes fréquences spatiales.
● Résolution de la caméra : Déterminée par le capteur, la résolution de la caméra dépend de la taille des pixels, du pas de pixel et des dimensions globales du capteur. Le pas de pixel d'uncaméra CMOSdéfinit directement sa fréquence de Nyquist, qui détermine le niveau de détail maximal que le capteur peut capturer.

Lorsque ces deux éléments ne sont pas alignés, des problèmes surviennent. Un objectif dont le pouvoir de résolution dépasse celui du capteur est un véritable gaspillage, car le capteur ne peut capturer tous les détails. À l'inverse, un capteur haute résolution associé à un objectif de mauvaise qualité produit des images qui ne s'améliorent pas malgré un nombre de mégapixels plus élevé.

Comment équilibrer la résolution optique et celle de l'appareil photo

L'équilibrage de l'optique et des capteurs consiste à faire correspondre la fréquence de Nyquist du capteur avec la fréquence de coupure optique de l'objectif.

● La fréquence de Nyquist d'un capteur de caméra est calculée comme suit : 1 / (2 × pas de pixel). Cela définit la fréquence spatiale la plus élevée que le capteur peut échantillonner sans crénelage.
● La fréquence de coupure optique dépend des caractéristiques de la lentille et de la diffraction.

Pour de meilleurs résultats, la fréquence de Nyquist du capteur doit correspondre à la résolution de l'objectif, voire la dépasser légèrement. En pratique, une bonne règle empirique consiste à s'assurer que le pas de pixel est environ la moitié de la plus petite taille résolvable de l'objectif.

Par exemple, si un objectif peut résoudre des détails jusqu’à 4 micromètres, alors un capteur avec des tailles de pixels d’environ 2 micromètres équilibrera bien le système.

Correspondance entre Nyquist et la résolution de l'appareil photo et le défi des pixels carrés

La diminution de la taille des pixels de l'espace objet se traduit par une diminution de la capacité de collecte de la lumière. Il est donc important de trouver un équilibre entre résolution et capacité de collecte de la lumière. De plus, des pixels plus grands dans l'espace objet offrent généralement un champ de vision plus large. Pour les applications nécessitant une résolution fine, un équilibre optimal est généralement trouvé : la taille des pixels de l'espace objet, multipliée par un facteur tenant compte de Nyquist, doit être égale à la résolution optique. Cette valeur est appelée résolution de la caméra.

L'équilibrage des optiques et des capteurs revient souvent à s'assurer que la résolution d'échantillonnage effective de la caméra correspond à la limite de résolution optique de l'objectif. On dit qu'un système est conforme à la norme de Nyquist lorsque :

Résolution de la caméra = Résolution optique

Où la résolution de la caméra est donnée par :

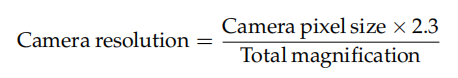
Formule de calcul de la résolution de la caméra

Le facteur à prendre en compte pour Nyquist qui est souvent recommandé est 2,3, et non 2. La raison en est la suivante.

Les pixels de la caméra sont (généralement) carrés et disposés sur une grille 2D. La taille des pixels, telle que définie dans l'équation ci-contre, représente la largeur des pixels le long des axes de cette grille. Si les entités à résoudre se trouvent à un angle autre qu'un multiple parfait de 90° par rapport à cette grille, la taille effective des pixels sera plus grande, jusqu'à √2 ≈ 1,41 fois la taille des pixels à 45°. Ceci est illustré dans la figure 2 (moitié inférieure).

Le facteur recommandé selon le critère de Nyquist, toutes orientations confondues, serait donc de 2√2 ≈ 2,82. Cependant, en raison du compromis mentionné précédemment entre résolution et captation de lumière, une valeur de compromis de 2,3 est recommandée en règle générale.

Le rôle de l'échantillonnage de Nyquist en imagerie

L'échantillonnage de Nyquist est le garant de la fidélité de l'image. Lorsque la fréquence d'échantillonnage descend sous la limite de Nyquist :

● Sous-échantillonnage→ provoque un aliasing : faux détails, bords irréguliers ou motifs moirés.

● Suréchantillonnage→ capture plus de données que ce que l'optique peut fournir, ce qui entraîne des rendements décroissants : des fichiers plus volumineux et des exigences de traitement plus élevées sans améliorations visibles.

Un échantillonnage correct garantit des images nettes et fidèles à la réalité. Il assure l'équilibre entre l'entrée optique et la capture numérique, évitant ainsi les pertes de résolution d'un côté et les artefacts trompeurs de l'autre.

Applications pratiques

L’échantillonnage de Nyquist n’est pas seulement une théorie : il a des applications critiques dans toutes les disciplines de l’imagerie :

●Microscopie:Les chercheurs doivent choisir des capteurs qui échantillonnent au moins deux fois le plus petit détail résolvable par l'objectif. Choisir le boncaméra de microscopieest cruciale, car la taille des pixels doit correspondre à la résolution limitée par la diffraction de l'objectif du microscope. Les laboratoires modernes privilégient souventcaméras sCMOS, qui offrent un équilibre entre sensibilité, plage dynamique et structures de pixels fines pour une imagerie biologique haute performance.

●AstronomieLes télescopes captent des signaux faibles et distants. L'association de capteurs et d'optiques garantit un niveau de détail maximal sans artefacts.

●Photographie: L'association de capteurs haute résolution à des objectifs incapables de reproduire des détails aussi fins entraîne souvent des améliorations négligeables de la netteté. Les photographes professionnels équilibrent objectifs et appareils photo pour éviter le gaspillage de résolution.

●Vision industrielle etCaméras scientifiques:En contrôle qualité et en inspection industrielle, l'absence de petites caractéristiques due à un sous-échantillonnage peut empêcher la détection de pièces défectueuses. Le suréchantillonnage peut être utilisé délibérément pour un zoom numérique ou un traitement amélioré.

Quand faire correspondre Nyquist : suréchantillonnage et sous-échantillonnage

L'échantillonnage de Nyquist représente l'équilibre idéal, mais dans la pratique, les systèmes d'imagerie peuvent intentionnellement suréchantillonner ou sous-échantillonner en fonction de l'application.

Qu'est-ce que le sous-échantillonnage

Dans le cas d'applications où la sensibilité prime sur la résolution des plus petits détails, l'utilisation d'une taille de pixel dans l'espace objet supérieure aux exigences de Nyquist peut offrir des avantages considérables en matière de collecte de lumière. C'est ce qu'on appelle le sous-échantillonnage.

Cela sacrifie les détails fins, mais peut être avantageux lorsque :

● La sensibilité est essentielle : les pixels plus grands collectent plus de lumière, améliorant ainsi le rapport signal/bruit dans l'imagerie en basse lumière.
● La vitesse est importante : moins de pixels réduisent le temps de lecture, permettant une acquisition plus rapide.
● L'efficacité des données est requise : des tailles de fichiers plus petites sont préférables dans les systèmes à bande passante limitée.

Exemple : dans l'imagerie du calcium ou de la tension, les signaux sont souvent moyennés sur les régions d'intérêt, de sorte que le sous-échantillonnage améliore la collecte de lumière sans compromettre le résultat scientifique.

Qu'est-ce que le suréchantillonnage

À l’inverse, de nombreuses applications pour lesquelles la résolution des détails fins est essentielle, ou des applications utilisant des méthodes d’analyse post-acquisition pour récupérer des informations supplémentaires au-delà de la limite de diffraction, nécessitent des pixels d’imagerie plus petits que ceux exigés par Nyquist, appelés suréchantillonnage.

Bien que cela n’augmente pas la véritable résolution optique, cela peut offrir des avantages :

● Permet un zoom numérique avec moins de perte de qualité.
● Améliore le post-traitement (par exemple, déconvolution, débruitage, super-résolution).
● Réduit l'aliasing visible lorsque les images sont sous-échantillonnées ultérieurement.

Exemple : En microscopie, une caméra sCMOS haute résolution peut suréchantillonner les structures cellulaires afin que les algorithmes de calcul puissent extraire des détails fins au-delà de la limite de diffraction.

Idées fausses courantes

1. Plus de mégapixels signifient toujours des images plus nettes.

Faux. La netteté dépend à la fois du pouvoir de résolution de l'objectif et de la qualité d'échantillonnage du capteur.

2. Tout bon objectif fonctionne bien avec n’importe quel capteur haute résolution.

Une mauvaise correspondance entre la résolution de l’objectif et le pas de pixel limitera les performances.

3、L'échantillonnage de Nyquist n'est pertinent que dans le traitement du signal, pas dans l'imagerie.

Au contraire, l’imagerie numérique est fondamentalement un processus d’échantillonnage, et Nyquist est ici aussi pertinent que dans l’audio ou les communications.

Conclusion

L'échantillonnage de Nyquist est plus qu'une abstraction mathématique : c'est le principe qui assure la synergie entre résolution optique et numérique. En alignant le pouvoir de résolution des lentilles sur les capacités d'échantillonnage des capteurs, les systèmes d'imagerie atteignent une clarté maximale sans artefacts ni perte de capacité.

Pour les professionnels de domaines aussi variés que la microscopie, l'astronomie, la photographie et la vision industrielle, la compréhension de l'échantillonnage de Nyquist est essentielle à la conception ou au choix de systèmes d'imagerie offrant des résultats fiables. En fin de compte, la qualité d'image ne résulte pas de la recherche d'une spécification à l'extrême, mais de la recherche d'un équilibre.

FAQ

Que se passe-t-il si l'échantillonnage de Nyquist n'est pas satisfait dans une caméra ?

Lorsque la fréquence d'échantillonnage descend en dessous de la limite de Nyquist, le capteur ne peut pas représenter correctement les détails fins. Cela entraîne un crénelage, qui se manifeste par des bords irréguliers, des moirés ou de fausses textures inexistantes dans la scène réelle.

Comment la taille des pixels affecte-t-elle l’échantillonnage de Nyquist ?

Des pixels plus petits augmentent la fréquence de Nyquist, ce qui signifie que le capteur peut théoriquement reproduire des détails plus fins. Mais si l'objectif ne peut pas offrir ce niveau de résolution, les pixels supplémentaires n'apportent que peu de valeur ajoutée et peuvent augmenter le bruit.

L'échantillonnage de Nyquist est-il différent pour les capteurs monochromes et couleur ?

Oui. Dans un capteur monochrome, chaque pixel échantillonne directement la luminance, de sorte que la fréquence de Nyquist effective correspond au pas de pixel. Dans un capteur couleur équipé d'un filtre de Bayer, chaque canal de couleur est sous-échantillonné, de sorte que la résolution effective après dématriçage est légèrement inférieure.