25/09/04I gcás íomháithe digiteacha, is furasta glacadh leis go gciallaíonn taifeach níos airde pictiúir níos fearr go huathoibríoch. Is minic a mhargaíonn monaróirí ceamaraí córais bunaithe ar chomhaireamh megapixel, agus leagann déantóirí lionsaí béim ar chumhacht réitigh agus géire. Ach, i gcleachtas, ní hamháin go mbraitheann cáilíocht na híomhá ar shonraíochtaí an lionsa nó an braiteora ina n-aonar ach freisin ar cé chomh maith agus a mheaitseálann siad.
Seo an áit a dtagann sampláil Nyquist i bhfeidhm. Prionsabal ó phróiseáil comharthaí ar dtús a bhí i gcritéar Nyquist, ach leagann sé síos an creat teoiriciúil chun sonraí a ghabháil go cruinn. San íomháú, cinntíonn sé go n-oibríonn an taifeach optúil a sheachadann lionsa agus an taifeach digiteach ó braiteoir ceamara le chéile go comhchuí.
Pléann an t-alt seo sampláil Nyquist i gcomhthéacs na híomháithe, míníonn sé an chothromaíocht idir réiteach optúil agus réiteach ceamara, agus soláthraíonn sé treoirlínte praiticiúla d'fheidhmchláir ó ghrianghrafadóireacht go híomháú eolaíoch.
Cad is Sampláil Nyquist ann?
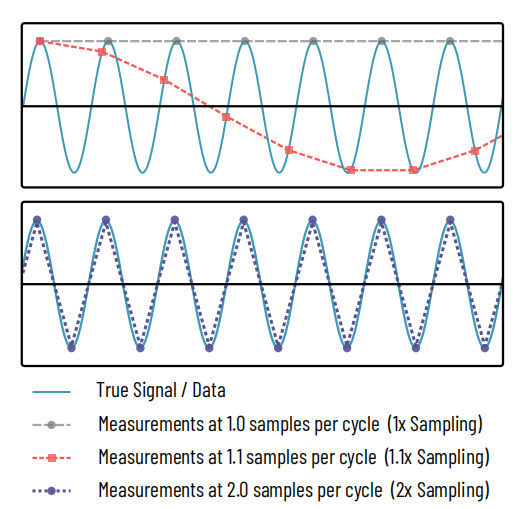
Fíor 1: Teoirim samplála Nyquist
BarrDéantar comhartha sinusoideach (cian) a thomhas, nó a sampláil, ag ilphointí. Léiríonn an líne liath fhada-phacáilte 1 tomhas in aghaidh an timthrialla den chomhartha sinusoideach, ag gabháil buaicphointí an chomhartha amháin, ag ceilt fíornádúr an chomhartha go hiomlán. Gabhann an cuar mín-phacáilte dearg 1.1 tomhas in aghaidh an tsampla, ag nochtadh sinusoid ach ag míléiriú a mhinicíochta. Tá sé seo cosúil le patrún Moiré.
BunNí thosaíonn fíornádúr an chomhartha á ghabháil ach amháin nuair a thógtar 2 shampla in aghaidh an timthrialla (líne poncaithe corcra).
Is prionsabal coitianta é teoirim samplála Nyquist i bpróiseáil comharthaí san leictreonaic, sa phróiseáil fuaime, san íomháú agus i réimsí eile. Déanann an teoirim soiléir gur gá tomhais a dhéanamh ar a laghad dhá oiread na minicíochta sin, mar a thaispeántar i bhFíor 1, chun minicíocht ar leith i gcomhartha a athchruthú. I gcás ár réitigh optúla, ciallaíonn sé seo nach mór go mbeadh méid picteilín ár spáis réada leath den mhionsonra is lú atáimid ag iarraidh a ghabháil ar a mhéad, nó, i gcás micreascóip, leath réiteach an mhicreascóip.
Fíor 2: Sampláil Nyquist le picteilíní cearnacha: tá tábhacht le treoshuíomh
Agus ceamara le greille de phicteilíní cearnacha á úsáid, ní ghabhfaidh fachtóir samplála 2x theoirim Nyquist ach sonraí atá ailínithe go foirfe leis an ngreille picteilíní go cruinn. Má dhéantar iarracht struchtúir a réiteach ag uillinn leis an ngreille picteilíní, tá an méid picteilíní éifeachtach níos mó, suas le √2 uair níos mó ag an trasnán. Dá bhrí sin, ní mór don ráta samplála a bheith 2√2 uair an mhinicíocht spásúil atá ag teastáil chun sonraí a ghabháil ag 45° leis an ngreille picteilíní.
Is léir an chúis atá leis seo trí bhreithniú a dhéanamh ar Fhíor 2 (an leath uachtarach). Samhlaigh go bhfuil méid an phicteilín socraithe go dtí an taifeach optúil, rud a thugann a bpicteilín féin do bhuaicphointí dhá fhoinse phointe comharsanacha, nó d'aon mhionsonra atáimid ag iarraidh a réiteach. Cé go mbraitear iad seo ar leithligh ansin, níl aon léiriú sna tomhais a eascraíonn as sin gur dhá bhuaic ar leithligh iad - agus arís eile ní chomhlíontar ár sainmhíniú ar "réiteach". Tá picteilín eatarthu ag teastáil, ag gabháil clais den chomhartha. Baintear é seo amach tríd an ráta samplála spásúil a dhúbailt ar a laghad, i.e. méid picteilín spáis an réada a laghdú faoi leath.
Rún Optúil vs. Rún Ceamara
Chun tuiscint a fháil ar an gcaoi a n-oibríonn sampláil Nyquist san íomháú, ní mór dúinn idirdhealú a dhéanamh idir dhá chineál réitigh:
● Taifeach Optúil: Cinntear taifeach optúil ag an lionsa, agus tagraíonn sé dá chumas mionsonraí mín a atáirgeadh. Socraíonn fachtóirí ar nós cáilíocht lionsa, cró, agus difreaction an teorainn seo. Is minic a úsáidtear an fheidhm aistrithe modhnúcháin (MTF) chun a thomhas cé chomh maith agus a tharchuireann lionsa codarsnacht ag minicíochtaí spásúla éagsúla.
● Réiteach Ceamara: Braitheann réiteach an cheamara, a chinntear ag an braiteoir, ar mhéid an phicteilín, ar pháirc an phicteilín, agus ar thoisí foriomlána an braiteora.Ceamara CMOSSainmhíníonn sé a mhinicíocht Nyquist go díreach, rud a chinneann an t-uasmhéid sonraí is féidir leis an braiteoir a ghabháil.
Nuair nach mbíonn an dá rud seo ailínithe, bíonn fadhbanna ann. Is éard atá i gceist le lionsa a sháraíonn cumhacht réitigh an braiteora ná "cur amú", ós rud é nach féidir leis an braiteoir na sonraí go léir a ghabháil. Os a choinne sin, bíonn íomhánna nach bhfeabhsaíonn in ainneoin níos mó megapixels mar thoradh ar lionsa ardtaifigh atá péireáilte le lionsa ísealchaighdeáin.
Conas Cothromaíocht a Bhaint as Rún Optúil agus Rún Ceamara
Ciallaíonn cothromaíocht a dhéanamh idir optaic agus braiteoirí go gcaithfear minicíocht Nyquist an braiteora a mheaitseáil le minicíocht scoir optúil an lionsa.
● Ríomhtar minicíocht Nyquist braiteora ceamara mar 1 / (2 × páirc picteilín). Sainmhíníonn sé seo an mhinicíocht spásúil is airde is féidir leis an braiteoir a shampláil gan ailiasú.
● Braitheann an mhinicíocht scoir optúil ar shaintréithe an lionsa agus ar an difreáil.
Chun na torthaí is fearr a fháil, ba chóir go mbeadh minicíocht Nyquist an braiteora ailínithe le cumas réitigh an lionsa nó beagán níos mó ná í. Go praiticiúil, is riail mhaith ordóige a chinntiú go bhfuil páirc an phicteilín thart ar leath mhéid gné inréitithe is lú an lionsa.
Mar shampla, más féidir le lionsa sonraí a réiteach síos go dtí 4 mhicriméadar, ansin déanfaidh braiteoir le méideanna picteilíní de ~2 mhicriméadar an córas a chothromú go maith.
Nyquist a Mheaitseáil le Rún Ceamara & Dúshlán na bPicteilíní Cearnógacha
Is é an chomhbhabhtáil le méid picteilín spás réada laghdaithe ná laghdú ar chumas bailithe solais. Dá bhrí sin, tá sé tábhachtach cothromaíocht a bhaint amach idir an gá atá le réiteach agus an gá atá le bailiú solais. Ina theannta sin, is gnách go dtugann méideanna picteilín spás réada níos mó réimse radhairc níos mó don ábhar íomháithe. I gcás feidhmchlár a bhfuil gá acu le réiteach mín, deirtear go mbaintear amach 'riail ordóige' mar seo a leanas: Ba chóir go mbeadh méid picteilín spás réada, nuair a iolraítear faoi fhachtóir éigin chun cuntas a thabhairt ar Nyquist, cothrom leis an réiteach optúil. Tugtar réiteach ceamara ar an gcainníocht seo.
Is minic a bhíonn cothromaíocht optaice agus braiteoirí ag brath ar a chinntiú go bhfuil réiteach samplála éifeachtach an cheamara ag teacht le teorainn réitigh optúil an lionsa. Deirtear go bhfuil córas "ag teacht le Nyquist" nuair:
Rún ceamara = Rún optúil
I gcás ina dtugtar taifeach an cheamara le:
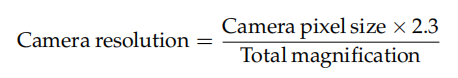
Is minic a mholtar 2.3, ní 2, chun Nyquist a chur san áireamh. Seo a leanas an chúis atá leis seo.
Is cearnach (de ghnáth) picteilíní ceamara, agus socraithe ar eangach 2-T. Léiríonn méid na bpicteilíní mar a shainmhínítear é lena úsáid sa chothromóid os coinne leithead na bpicteilíní feadh aiseanna an eangaigh seo. Má bhíonn na gnéithe atáimid ag iarraidh a réiteach suite ag aon uillinn seachas iolraí foirfe de 90° i gcoibhneas leis an eangach seo, beidh an méid picteilíní éifeachtach níos mó, suas le √2 ≈ 1.41 uair mhéid an phicteilíní ag 45°. Taispeántar é seo i bhFíor 2 (leath bun).
Dá bhrí sin, bheadh an fachtóir molta de réir chritéar Nyquist i ngach treoshuíomh 2√2 ≈ 2.82. Mar sin féin, mar gheall ar an gcomhbhabhtáil a luadh roimhe seo idir réiteach agus bailiú solais, moltar luach comhréitigh de 2.3 mar riail ordóige.
Ról Samplála Nyquist san Íomháú
Is í sampláil Nyquist geata na dílseachta íomhá. Nuair a thiteann an ráta samplála faoi bhun theorainn Nyquist:
● Fo-shampláil→ is cúis le hailiasú: sonraí bréagacha, imill gharbha, nó patrúin moiré.
● Ró-shampláil→ gabhann sé níos mó sonraí ná mar is féidir leis an optaic a sheachadadh, rud a fhágann go laghdaíonn an toradh: comhaid níos mó agus éilimh phróiseála níos airde gan feabhsuithe le feiceáil.
Cinntíonn sampláil cheart go bhfuil na híomhánna géar agus fíor don réaltacht araon. Soláthraíonn sé an chothromaíocht idir ionchur optúil agus gabháil dhigiteach, rud a sheachnaíonn rún amú ar thaobh amháin nó déantáin mhíthreoracha ar an taobh eile.
Feidhmeanna Praiticiúla
Ní teoiric amháin atá i gceist le sampláil Nyquist — tá feidhmeanna ríthábhachtacha aici i ndisciplíní íomháithe:
●MicreascópachtNí mór do thaighdeoirí braiteoirí a roghnú a dhéanann sampláil ar a laghad faoi dhó ar an mionsonra is lú is féidir a réiteach leis an lionsa cuspóir. An ceann ceart a roghnúceamara micreascópachtaríthábhachtach, mar ní mór méid na bpicteilíní a bheith ailínithe leis an taifeach atá teoranta ag difreacht cuspóir an mhicreascóip. Is minic a bhíonn rogha ag saotharlanna nua-aimsearthaceamaraí sCMOS, a sholáthraíonn cothromaíocht íogaireachta, raoin dinimiciúil, agus struchtúir picteilíní míne le haghaidh íomháú bitheolaíoch ardfheidhmíochta.
●RéalteolaíochtGabhann teileascóip comharthaí laga, i bhfad i gcéin. Cinntíonn meaitseáil braiteoirí le optaic teileascóip an méid mionsonraí is féidir gan aon déantáin a chur i láthair.
●GrianghrafadóireachtIs minic nach mbíonn mórán feabhsuithe ar ghéire mar thoradh ar braiteoirí ard-megapixel a phéireáil le lionsaí nach féidir leo sonraí chomh mín céanna a réiteach. Cothromaíonn grianghrafadóirí gairmiúla lionsaí agus ceamaraí chun rún caillte a sheachaint.
●Fís Meaisín &Ceamaraí EolaíochtaI rialú cáilíochta agus i gcigireacht thionsclaíoch, d’fhéadfadh sé nach mbeadh codanna lochtacha faoi deara má bhíonn gnéithe beaga ar iarraidh mar gheall ar easnamh samplála. Féadfar róshampláil a úsáid d’aon ghnó le haghaidh súmáil dhigitigh nó próiseála feabhsaithe.
Cathain is Ceart Nyquist a Mheaitseáil: Ró-shampláil agus Fo-shampláil
Is ionann sampláil Nyquist agus an chothromaíocht idéalach, ach i gcleachtas, féadfaidh córais íomháithe róshampláil nó tearcshampláil d'aon ghnó ag brath ar an bhfeidhmchlár.
Cad is Fo-shampláil ann
I gcás feidhmchlár ina bhfuil íogaireacht níos tábhachtaí ná na sonraí is lú a réiteach, is féidir buntáistí suntasacha bailiúcháin solais a bhaint amach trí mhéid picteilín spáis réada a úsáid atá níos mó ná mar a éilíonn Nyquist. Tugtar tearc-shampláil air seo.
Íobairtíonn sé seo mionsonraí, ach is féidir go mbeadh buntáiste leis nuair:
● Tá an íogaireacht ríthábhachtach: bailíonn picteilíní níos mó níos mó solais, rud a fheabhsaíonn an cóimheas comhartha-le-torann in íomháú i solas íseal.
● Tá luas tábhachtach: laghdaíonn níos lú picteilíní an t-am léite, rud a chuireann ar chumas fáil níos tapúla.
● Tá éifeachtúlacht sonraí ag teastáil: is fearr méideanna comhad níos lú i gcórais atá teoranta ó thaobh bandaleithead de.
Sampla: In íomháú cailciam nó voltais, is minic a dhéantar meánú ar chomharthaí thar réigiúin spéise, mar sin feabhsaíonn tearc-shampláil bailiú solais gan cur isteach ar an toradh eolaíoch.
Cad is Ró-shampláil ann
Os a choinne sin, bíonn picteilíní íomháithe níos lú ná mar a éilíonn Nyquist ag teastáil i go leor feidhmchlár ina bhfuil réiteach sonraí míne ríthábhachtach, nó feidhmchláir a úsáideann modhanna anailíse iar-fhála chun faisnéis bhreise a aisghabháil thar an teorainn difreactachta, ar a dtugtar róshampláil.
Cé nach méadaíonn sé seo fíor-réiteach optúil, is féidir leis buntáistí a sholáthar:
● Cumasaíonn sé súmáil dhigiteach le níos lú caillteanais cáilíochta.
● Feabhsaíonn sé iarphróiseáil (m.sh., díchonbhlúireacht, dí-torannú, sár-réiteach).
● Laghdaíonn sé ailiasú infheicthe nuair a dhéantar íosshampláil ar íomhánna níos déanaí.
Sampla: I micreascópacht, féadfaidh ceamara sCMOS ardtaifigh ró-shampláil a dhéanamh ar struchtúir cheallacha ionas gur féidir le halgartaim ríomhaireachtúla sonraí míne a bhaint amach thar an teorainn difreactachta.
Míthuiscintí Coitianta
1. Ciallaíonn níos mó megapixels íomhánna níos géire i gcónaí.
Ní fíor. Braitheann géire ar chumhacht réitigh an lionsa agus ar cibé an ndéanann an braiteoir sampláil i gceart.
2. Oibríonn aon lionsa maith go maith le haon braiteoir ardtaifigh.
Cuirfidh droch-chomhoiriúnú idir réiteach an lionsa agus páirc na bpicteilíní teorainn leis an bhfeidhmíocht.
3. Níl sampláil Nyquist ábhartha ach i bpróiseáil comharthaí, ní san íomháú.
Os a choinne sin, is próiseas samplála go bunúsach í an íomháú digiteach, agus tá Nyquist chomh hábhartha anseo agus atá sé i gcás fuaime nó cumarsáide.
Conclúid
Is mó ná teibí matamaiticiúil é sampláil Nyquist — is é an prionsabal a chinntíonn go n-oibríonn réiteach optúil agus digiteach le chéile. Trí chumhacht réitigh lionsaí a ailíniú le cumais samplála braiteoirí, baintear amach soiléireacht uasta i gcórais íomháithe gan aon déantáin ná acmhainneacht amú.
I gcás gairmithe i réimsí chomh héagsúil le micreascópacht, réalteolaíocht, grianghrafadóireacht, agus fís meaisín, is í an eochair chun córais íomháithe a dhearadh nó a roghnú a thugann torthaí iontaofa tuiscint a fháil ar shampláil Nyquist. Sa deireadh thiar, ní ó shonraíocht amháin a bhrú go dtí an pointe is airde a thagann cáilíocht íomhá ach ó chothromaíocht a bhaint amach.
Ceisteanna Coitianta
Cad a tharlaíonn mura gcomhlíontar sampláil Nyquist i gceamara?
Nuair a thiteann an ráta samplála faoi bhun theorainn Nyquist, ní féidir leis an braiteoir sonraí míne a léiriú i gceart. Mar thoradh air sin, bíonn aliasing ann, a fheictear mar imill gharbha, patrúin moiré, nó uigeachtaí bréagacha nach bhfuil ann sa radharc fíor.
Cén tionchar a bhíonn ag méid picteilín ar shampláil Nyquist?
Méadaíonn picteilíní níos lú minicíocht Nyquist, rud a chiallaíonn gur féidir leis an braiteoir sonraí níos míne a réiteach go teoiriciúil. Ach mura féidir leis an lionsa an leibhéal réitigh sin a sheachadadh, ní chuireann na picteilíní breise mórán luacha leis agus féadfaidh siad torann a mhéadú.
An bhfuil sampláil Nyquist difriúil do braiteoirí monacrómacha vs. braiteoirí datha?
Sea. I braiteoir monacrómach, déanann gach picteilín sampláil dhíreach ar an lonrachas, mar sin bíonn minicíocht éifeachtach Nyquist ag teacht le páirc an phicteilín. I braiteoir datha le scagaire Bayer, déantar tearcshampláil ar gach cainéal datha, mar sin bíonn an taifeach éifeachtach tar éis dí-shamplála beagán níos ísle.
Tucsen Photonics Co., Ltd. Gach ceart ar cosaint. Agus tú ag lua, luaigh an fhoinse le do thoil:www.tucsen.com
