Na imaxe dixital, é doado asumir que unha maior resolución significa automaticamente mellores imaxes. Os fabricantes de cámaras adoitan comercializar sistemas baseados no número de megapíxeles, mentres que os fabricantes de lentes destacan o poder de resolución e a nitidez. Con todo, na práctica, a calidade da imaxe non só depende das especificacións da lente ou do sensor individualmente, senón tamén de como de ben se axustan.
Aquí é onde entra en xogo a mostraxe de Nyquist. Orixinalmente un principio do procesamento de sinais, o criterio de Nyquist establece o marco teórico para capturar detalles con precisión. Na imaxe, garante que a resolución óptica proporcionada por unha lente e a resolución dixital do sensor dunha cámara funcionen conxuntamente de forma harmoniosa.
Este artigo analiza a mostraxe de Nyquist no contexto da obtención de imaxes, explica o equilibrio entre a resolución óptica e a da cámara e proporciona pautas prácticas para aplicacións que van dende a fotografía ata a obtención de imaxes científicas.
Que é a mostraxe de Nyquist?
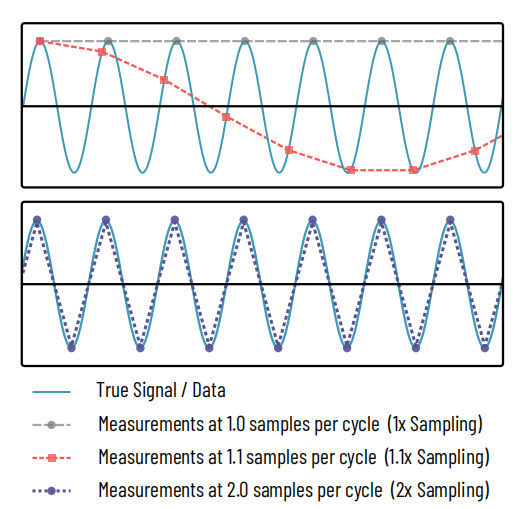
Figura 1: O teorema de mostraxe de Nyquist
Arriba:Mídese ou muestrease un sinal sinusoidal (cian) en varios puntos. A liña gris de trazos longos representa 1 medición por ciclo do sinal sinusoidal, capturando só os picos do sinal, ocultando completamente a verdadeira natureza do sinal. A curva vermella de trazos finos captura 1,1 medicións por mostra, revelando unha sinusoide pero representando mal a súa frecuencia. Isto é análogo a un patrón Moiré.
Parte inferior:Só cando se toman 2 mostras por ciclo (liña punteada morada) comeza a captarse a verdadeira natureza do sinal.
O teorema de mostraxe de Nyquist é un principio común no procesamento de sinais en electrónica, procesamento de son, imaxe e outros campos. O teorema deixa claro que para reconstruír unha frecuencia determinada nun sinal, as medicións deben realizarse polo menos o dobre desa frecuencia, como se mostra na Figura 1. No caso da nosa resolución óptica, isto significa que o tamaño de píxel do noso espazo de obxectos debe ser como máximo a metade do detalle máis pequeno que estamos a tentar capturar ou, no caso dun microscopio, a metade da resolución do microscopio.
Figura 2: Mostraxe de Nyquist con píxeles cadrados: a orientación importa
Usando unha cámara cunha grella de píxeles cadrados, o factor de mostraxe 2x do teorema de Nyquist só capturará con precisión os detalles que estean perfectamente aliñados coa grella de píxeles. Se se tenta resolver estruturas nun ángulo con respecto á grella de píxeles, o tamaño efectivo do píxel é maior, ata √2 veces maior na diagonal. Polo tanto, a taxa de mostraxe debe ser 2√2 veces a frecuencia espacial desexada para capturar detalles a 45o con respecto á grella de píxeles.
A razón disto faise obvia ao considerar a Figura 2 (metade superior). Imaxina que o tamaño do píxel se axusta á resolución óptica, dando aos picos de dúas fontes puntuais veciñas, ou calquera detalle que esteamos a intentar resolver, cada un o seu propio píxel. Aínda que estes se detectan por separado, non hai ningunha indicación nas medicións resultantes de que sexan dous picos separados e, unha vez máis, non se cumpre a nosa definición de "resolución". Necesítase un píxel no medio, capturando un mínimo do sinal. Isto conséguese polo menos duplicando a taxa de mostraxe espacial, é dicir, reducindo á metade o tamaño do píxel do espazo do obxecto.
Resolución óptica fronte á resolución da cámara
Para comprender como funciona a mostraxe de Nyquist na obtención de imaxes, debemos distinguir entre dous tipos de resolución:
● Resolución óptica: Determinada pola lente, a resolución óptica refírese á súa capacidade para reproducir detalles finos. Factores como a calidade da lente, a apertura e a difracción establecen este límite. A función de transferencia de modulación (MTF) úsase a miúdo para medir o ben que unha lente transmite o contraste a diferentes frecuencias espaciais.
● Resolución da cámara: Determinada polo sensor, a resolución da cámara depende do tamaño do píxel, do paso entre píxeles e das dimensións xerais do sensor. O paso entre píxeles duncámara CMOSdefine directamente a súa frecuencia de Nyquist, que determina o detalle máximo que o sensor pode capturar.
Cando estes dous non están aliñados, xorden problemas. Unha lente que supera o poder de resolución do sensor está practicamente "desperdiciada", xa que o sensor non pode capturar todos os detalles. Pola contra, un sensor de alta resolución combinado cunha lente de baixa calidade dá lugar a imaxes que non melloran a pesar de ter máis megapíxeles.
Como equilibrar a resolución óptica e a da cámara
Equilibrar a óptica e os sensores significa axustar a frecuencia de Nyquist do sensor coa frecuencia de corte óptica da lente.
● A frecuencia de Nyquist dun sensor de cámara calcúlase como 1 / (2 × paso de píxel). Isto define a frecuencia espacial máis alta que o sensor pode muestrear sen aliasing.
● A frecuencia de corte óptico depende das características da lente e da difracción.
Para obter mellores resultados, a frecuencia de Nyquist do sensor debe aliñarse coa capacidade de resolución da lente ou superarla lixeiramente. Na práctica, unha boa regra xeral é garantir que o paso entre píxeles sexa aproximadamente a metade do tamaño de característica resoluble máis pequeno da lente.
Por exemplo, se unha lente pode resolver detalles de ata 4 micrómetros, un sensor con tamaños de píxel de ~2 micrómetros equilibrará ben o sistema.
Emparellando Nyquist coa resolución da cámara e o desafío dos píxeles cadrados
A contrapartida da diminución do tamaño dos píxeles no espazo do obxecto é a redución da capacidade de recollida de luz. Polo tanto, é importante equilibrar a necesidade de resolución e a recollida de luz. Ademais, os tamaños de píxeles no espazo do obxecto máis grandes tenden a transmitir un campo de visión máis amplo do suxeito da imaxe. Para aplicacións que precisan unha resolución fina, dise que se alcanza unha "regra xeral" de equilibrio óptimo do seguinte xeito: o tamaño do píxel no espazo do obxecto, cando se multiplica por algún factor para ter en conta o teorema de Nyquist, debe ser igual á resolución óptica. Esta cantidade denomínase resolución da cámara.
O equilibrio entre a óptica e os sensores adoita reducirse a garantir que a resolución de mostraxe efectiva da cámara coincida co límite de resolución óptica da lente. Dise que un sistema "coincide con Nyquist" cando:
Resolución da cámara = Resolución óptica
Onde a resolución da cámara vén dada por:
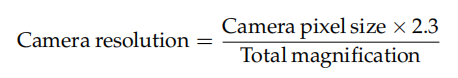
O factor para ter en conta o coeficiente de Nyquist que se recomenda a miúdo é 2,3, non 2. A razón disto é a seguinte.
Os píxeles da cámara son (normalmente) cadrados e están dispostos nunha grella bidimensional. O tamaño do píxel, tal como se define para o seu uso na ecuación oposta, representa o ancho dos píxeles ao longo dos eixes desta grella. Se as características que estamos a tentar resolver se atopan en calquera ángulo que non sexa un múltiplo perfecto de 90° en relación con esta grella, o tamaño efectivo do píxel será maior, ata √2 ≈ 1,41 veces o tamaño do píxel a 45°. Isto móstrase na Figura 2 (metade inferior).
Polo tanto, o factor recomendado segundo o criterio de Nyquist en todas as orientacións sería 2√2 ≈ 2,82. Non obstante, debido á compensación mencionada anteriormente entre a resolución e a recollida de luz, recoméndase un valor de compromiso de 2,3 como regra xeral.
O papel da mostraxe de Nyquist na obtención de imaxes
A mostraxe de Nyquist é o gardián da fidelidade da imaxe. Cando a taxa de mostraxe cae por debaixo do límite de Nyquist:
● Submostraxe → provoca aliasing: detalles falsos, bordos irregulares ou patróns moiré.
● Sobremostraxe → captura máis datos dos que a óptica pode fornecer, o que leva a rendementos decrecentes: ficheiros máis grandes e maiores demandas de procesamento sen melloras visibles.
Unha mostraxe correcta garante que as imaxes sexan nítidas e fieis á realidade. Proporciona o equilibrio entre a entrada óptica e a captura dixital, evitando a resolución perdida nun lado ou artefactos enganosos no outro.
Aplicacións prácticas
A mostraxe de Nyquist non é só teoría: ten aplicacións críticas en todas as disciplinas da imaxe:
● Microscopía:Os investigadores deben escoller sensores que mostren polo menos o dobre do detalle máis pequeno que pode resolver a lente obxectiva. Escollendo o correctocámara de microscopíaé fundamental, xa que o tamaño do píxel debe aliñarse coa resolución limitada por difracción do obxectivo do microscopio. Os laboratorios modernos adoitan preferircámaras sCMOS, que proporcionan un equilibrio entre sensibilidade, rango dinámico e estruturas finas de píxeles para a obtención de imaxes biolóxicas de alto rendemento.

● Fotografía:Emparellar sensores de alta resolución con lentes que non poden resolver detalles igualmente finos adoita resultar en melloras insignificantes na nitidez. Os fotógrafos profesionais equilibran as lentes e as cámaras para evitar unha resolución desperdiciada.
● Fotografía:Emparellar sensores de alta resolución con lentes que non poden resolver detalles igualmente finos adoita resultar en melloras insignificantes na nitidez. Os fotógrafos profesionais equilibran as lentes e as cámaras para evitar unha resolución desperdiciada.
● Visión artificial eCámaras científicasNo control de calidade e na inspección industrial, a falta de pequenas características debido á submostraxe podería significar que as pezas defectuosas pasen desapercibidas. A sobremostraxe pódese usar deliberadamente para o zoom dixital ou o procesamento mellorado.
Cando coincidir con Nyquist: sobremostraxe e submostraxe
A mostraxe de Nyquist representa o equilibrio ideal, pero na práctica, os sistemas de imaxe poden sobremostrar ou submostrar intencionadamente dependendo da aplicación.
Que é a submostraxe
No caso de aplicacións onde a sensibilidade é máis importante que a resolución dos detalles máis pequenos, o uso dun tamaño de píxel no espazo do obxecto que sexa maior que as esixencias de Nyquist pode levar a vantaxes considerables na recollida de luz. Isto chámase submostraxe.
Isto sacrifica os detalles finos, pero pode ser vantaxoso cando:
● A sensibilidade é fundamental: os píxeles máis grandes recollen máis luz, o que mellora a relación sinal-ruído nas imaxes con pouca luz.
● A velocidade importa: un menor número de píxeles reduce o tempo de lectura, o que permite unha adquisición máis rápida.
● É necesaria eficiencia nos datos: os tamaños de ficheiro máis pequenos son preferibles en sistemas con ancho de banda limitado.
Exemplo: Na obtención de imaxes de calcio ou voltaxe, os sinais adoitan calcularse como media sobre as rexións de interese, polo que a submostraxe mellora a recollida de luz sen comprometer o resultado científico.
Que é a sobremostraxe
Pola contra, moitas aplicacións para as que a resolución de detalles finos é fundamental, ou aplicacións que empregan métodos de análise posadquisición para recuperar información adicional máis alá do límite de difracción, requiren píxeles de imaxe máis pequenos que os esixidos por Nyquist, o que se denomina sobremostraxe.
Aínda que isto non aumenta a resolución óptica real, pode ofrecer vantaxes:
● Activa o zoom dixital con menos perda de calidade.
● Mellora o posprocesamento (por exemplo, deconvolución, eliminación de ruído, superresolución).
● Reduce o aliasing visible cando as imaxes se reducen posteriormente.
Exemplo: En microscopía, unha cámara sCMOS de alta resolución pode sobremostrar estruturas celulares para que os algoritmos computacionais poidan extraer detalles finos máis alá do límite de difracción.
Conceptos erróneos comúns
1. Máis megapíxeles sempre significan imaxes máis nítidas.
Non é certo. A nitidez depende tanto do poder de resolución da lente como de se o sensor realiza a mostraxe axeitada.
2. Calquera boa lente funciona ben con calquera sensor de alta resolución.
Unha mala correspondencia entre a resolución da lente e o paso entre píxeles limitará o rendemento.
3. A mostraxe de Nyquist só é relevante no procesamento de sinais, non na obtención de imaxes.
Pola contra, a imaxe dixital é fundamentalmente un proceso de mostraxe, e Nyquist é tan relevante aquí como no audio ou nas comunicacións.
Conclusión
A mostraxe de Nyquist é máis que unha abstracción matemática: é o principio que garante que a resolución óptica e a dixital funcionen conxuntamente. Ao aliñar o poder de resolución das lentes coas capacidades de mostraxe dos sensores, os sistemas de imaxe conseguen a máxima claridade sen artefactos nin capacidade desperdiciada.
Para profesionais de campos tan diversos como a microscopía, a astronomía, a fotografía e a visión artificial, comprender a mostraxe de Nyquist é fundamental para deseñar ou elixir sistemas de imaxe que ofrezan resultados fiables. En definitiva, a calidade da imaxe non provén de levar unha especificación ao extremo, senón de acadar o equilibrio.
Preguntas frecuentes
Que ocorre se unha cámara non cumpre a mostraxe de Nyquist?
Cando a taxa de mostraxe cae por debaixo do límite de Nyquist, o sensor non pode representar correctamente os detalles finos. Isto provoca un efecto de aliasing, que aparece como bordos irregulares, patróns moiré ou texturas falsas que non existen na escena real.
Como afecta o tamaño dos píxeles á mostraxe de Nyquist?
Os píxeles máis pequenos aumentan a frecuencia de Nyquist, o que significa que o sensor pode resolver teoricamente detalles máis finos. Pero se a lente non pode ofrecer ese nivel de resolución, os píxeles adicionais engaden pouco valor e poden aumentar o ruído.
É diferente a mostraxe de Nyquist para sensores monocromos e de cor?
Si. Nun sensor monocromático, cada píxel toma mostras de luminancia directamente, polo que a frecuencia efectiva de Nyquist coincide co paso do píxel. Nun sensor de cor cun filtro de Bayer, cada canle de cor está submostrada, polo que a resolución efectiva despois da desmostraxe é lixeiramente menor.
Tucsen Photonics Co., Ltd. Todos os dereitos reservados. Ao citar, indique a fonte:www.tucsen.com

 25/09/04
25/09/04