25/09/04Nell'imaging digitale, è facile presumere che una risoluzione più elevata significhi automaticamente immagini migliori. I produttori di fotocamere spesso commercializzano sistemi basati sul numero di megapixel, mentre i produttori di obiettivi sottolineano il potere risolvente e la nitidezza. Tuttavia, nella pratica, la qualità dell'immagine dipende non solo dalle specifiche dell'obiettivo o del sensore singolarmente, ma anche da quanto questi siano ben abbinati.
È qui che entra in gioco il campionamento di Nyquist. Originariamente un principio dell'elaborazione del segnale, il criterio di Nyquist definisce il quadro teorico per catturare i dettagli in modo accurato. Nell'imaging, garantisce che la risoluzione ottica fornita da un obiettivo e la risoluzione digitale del sensore di una fotocamera funzionino insieme in modo armonioso.
Questo articolo analizza il campionamento di Nyquist nel contesto dell'imaging, spiega l'equilibrio tra risoluzione ottica e risoluzione della fotocamera e fornisce linee guida pratiche per applicazioni che spaziano dalla fotografia all'imaging scientifico.
Che cos'è il campionamento di Nyquist?
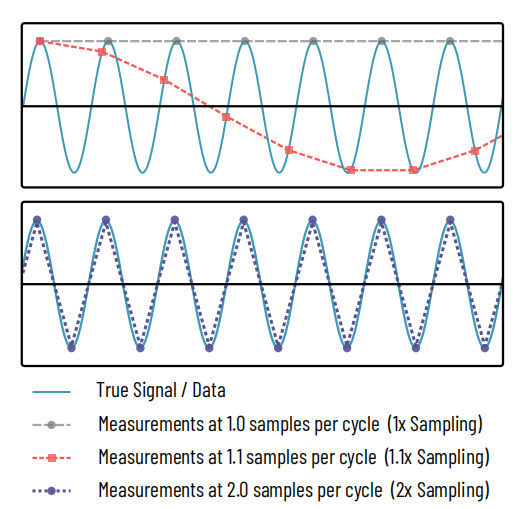
Figura 1: Il teorema del campionamento di Nyquist
Superiore: Un segnale sinusoidale (ciano) viene misurato, o campionato, in più punti. La linea grigia tratteggiata rappresenta 1 misurazione per ciclo del segnale sinusoidale, catturando solo i picchi del segnale e nascondendo completamente la vera natura del segnale. La curva rossa tratteggiata cattura 1,1 misurazioni per campione, rivelando una sinusoide ma travisandone la frequenza. Questo è analogo a un effetto Moiré.
Metter il fondo a: Solo quando vengono prelevati 2 campioni per ciclo (linea tratteggiata viola) si inizia a catturare la vera natura del segnale.
Il teorema del campionamento di Nyquist è un principio comune all'elaborazione del segnale in elettronica, elaborazione audio, imaging e altri campi. Il teorema chiarisce che per ricostruire una data frequenza in un segnale, le misurazioni devono essere effettuate a una frequenza almeno doppia rispetto a quella specifica, come mostrato in Figura 1. Nel caso della nostra risoluzione ottica, ciò significa che la dimensione dei pixel nello spazio oggetto deve essere al massimo pari alla metà del più piccolo dettaglio che stiamo cercando di catturare o, nel caso di un microscopio, pari alla metà della risoluzione del microscopio stesso.
Figura 2: Campionamento di Nyquist con pixel quadrati: l'orientamento è importante
Utilizzando una telecamera con una griglia di pixel quadrati, il fattore di campionamento 2x del teorema di Nyquist catturerà accuratamente solo i dettagli perfettamente allineati alla griglia di pixel. Se si tenta di risolvere strutture angolate rispetto alla griglia di pixel, la dimensione effettiva dei pixel è maggiore, fino a √2 volte maggiore sulla diagonale. La frequenza di campionamento deve quindi essere 2√2 volte la frequenza spaziale desiderata per catturare dettagli a 45° rispetto alla griglia di pixel.
Il motivo è reso evidente dall'analisi della Figura 2 (metà superiore). Immaginiamo che la dimensione dei pixel sia impostata sulla risoluzione ottica, assegnando ai picchi di due sorgenti puntiformi adiacenti, o a qualsiasi dettaglio che stiamo cercando di risolvere, un pixel a sé stante. Sebbene questi vengano poi rilevati separatamente, non vi è alcuna indicazione nelle misurazioni risultanti che si tratti di due picchi separati – e ancora una volta la nostra definizione di "risoluzione" non è soddisfatta. È necessario un pixel intermedio, che catturi una parte minima del segnale. Questo si ottiene almeno raddoppiando la frequenza di campionamento spaziale, ovvero dimezzando la dimensione dei pixel nello spazio oggetto.
Risoluzione ottica vs. risoluzione della fotocamera
Per comprendere il funzionamento del campionamento di Nyquist nell'imaging, dobbiamo distinguere due tipi di risoluzione:
● Risoluzione ottica: determinata dall'obiettivo, la risoluzione ottica si riferisce alla sua capacità di riprodurre dettagli fini. Fattori come la qualità dell'obiettivo, l'apertura e la diffrazione stabiliscono questo limite. La funzione di trasferimento della modulazione (MTF) viene spesso utilizzata per misurare l'efficacia della trasmissione del contrasto da parte di un obiettivo a diverse frequenze spaziali.
● Risoluzione della fotocamera: determinata dal sensore, la risoluzione della fotocamera dipende dalla dimensione dei pixel, dal passo dei pixel e dalle dimensioni complessive del sensore. Il passo dei pixel di unaFotocamera CMOSdefinisce direttamente la sua frequenza di Nyquist, che determina il massimo dettaglio che il sensore può catturare.
Quando questi due non sono allineati, sorgono problemi. Un obiettivo che supera il potere risolutivo del sensore è di fatto "sprecato", poiché il sensore non riesce a catturare tutti i dettagli. Al contrario, un sensore ad alta risoluzione abbinato a un obiettivo di bassa qualità produce immagini che non migliorano nonostante un numero maggiore di megapixel.
Come bilanciare la risoluzione ottica e quella della fotocamera
Per bilanciare ottica e sensori è necessario adattare la frequenza di Nyquist del sensore alla frequenza di taglio ottica della lente.
● La frequenza di Nyquist di un sensore di una fotocamera è calcolata come 1/(2 × pixel pitch). Questo definisce la frequenza spaziale più alta che il sensore può campionare senza aliasing.
● La frequenza di taglio ottica dipende dalle caratteristiche della lente e dalla diffrazione.
Per risultati ottimali, la frequenza di Nyquist del sensore dovrebbe essere allineata o leggermente superiore alla capacità di risoluzione dell'obiettivo. In pratica, una buona regola pratica è assicurarsi che il pixel pitch sia circa la metà della dimensione minima risolvibile dell'obiettivo.
Ad esempio, se una lente riesce a risolvere dettagli fino a 4 micrometri, un sensore con pixel di dimensioni pari a circa 2 micrometri bilancerà bene il sistema.
Abbinamento di Nyquist con la risoluzione della fotocamera e la sfida dei pixel quadrati
Il compromesso con la riduzione delle dimensioni dei pixel nello spazio oggetto è una minore capacità di raccolta della luce. È quindi importante bilanciare l'esigenza di risoluzione e quella di raccolta della luce. Inoltre, dimensioni maggiori dei pixel nello spazio oggetto tendono a trasmettere un campo visivo più ampio del soggetto ripreso. Per le applicazioni che richiedono una risoluzione elevata, si ritiene che il bilanciamento ottimale sia il seguente: la dimensione dei pixel nello spazio oggetto, moltiplicata per un fattore che tenga conto della legge di Nyquist, dovrebbe essere uguale alla risoluzione ottica. Questa quantità è chiamata risoluzione della fotocamera.
Il bilanciamento tra ottiche e sensori spesso si riduce a garantire che la risoluzione di campionamento effettiva della telecamera corrisponda al limite di risoluzione ottica dell'obiettivo. Si dice che un sistema "corrisponda alla legge di Nyquist" quando:
Risoluzione della fotocamera = Risoluzione ottica
Dove la risoluzione della telecamera è data da:
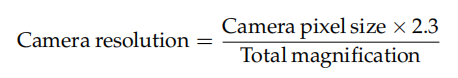
Il fattore di Nyquist spesso raccomandato è 2,3 e non 2. Il motivo è il seguente.
I pixel della fotocamera sono (tipicamente) quadrati e disposti su una griglia 2D. La dimensione dei pixel, come definita nell'equazione a lato, rappresenta la larghezza dei pixel lungo gli assi di questa griglia. Se le caratteristiche che stiamo cercando di risolvere si trovano a un angolo diverso da un multiplo perfetto di 90° rispetto a questa griglia, la dimensione effettiva dei pixel sarà maggiore, fino a √2 ≈ 1,41 volte la dimensione dei pixel a 45°. Questo è mostrato nella Figura 2 (metà inferiore).
Il fattore raccomandato secondo il criterio di Nyquist in tutti gli orientamenti sarebbe quindi 2√2 ≈ 2,82. Tuttavia, a causa del compromesso menzionato in precedenza tra risoluzione e raccolta della luce, si consiglia come regola generale un valore di compromesso di 2,3.
Il ruolo del campionamento di Nyquist nell'imaging
Il campionamento di Nyquist è il custode della fedeltà dell'immagine. Quando la frequenza di campionamento scende al di sotto del limite di Nyquist:
● Sottocampionamento→ provoca aliasing: dettagli falsi, bordi frastagliati o motivi moiré.
● Sovracampionamento→ cattura più dati di quanti l'ottica possa fornire, con conseguenti rendimenti decrescenti: file più grandi e richieste di elaborazione più elevate senza miglioramenti visibili.
Un campionamento corretto garantisce che le immagini siano nitide e fedeli alla realtà. Garantisce l'equilibrio tra input ottico e acquisizione digitale, evitando sprechi di risoluzione da un lato e artefatti fuorvianti dall'altro.
Applicazioni pratiche
Il campionamento di Nyquist non è solo teoria: ha applicazioni cruciali in tutte le discipline dell'imaging:
●Microscopia: I ricercatori devono scegliere sensori che campionano almeno il doppio del dettaglio più piccolo risolvibile dalla lente dell'obiettivo. Scegliere il sensore giustotelecamera per microscopiaè fondamentale, poiché la dimensione dei pixel deve essere allineata con la risoluzione limitata dalla diffrazione dell'obiettivo del microscopio. I laboratori moderni spesso preferisconotelecamere sCMOS, che forniscono un equilibrio tra sensibilità, gamma dinamica e strutture di pixel fini per l'imaging biologico ad alte prestazioni.
●Astronomia: I telescopi catturano segnali deboli e distanti. L'abbinamento dei sensori con le ottiche del telescopio garantisce il massimo dettaglio senza introdurre artefatti.
●Fotografia: L'abbinamento di sensori ad alta risoluzione con obiettivi che non riescono a risolvere dettagli altrettanto fini spesso si traduce in miglioramenti trascurabili della nitidezza. I fotografi professionisti bilanciano obiettivi e fotocamere per evitare sprechi di risoluzione.
●Visione artificiale eFotocamere scientifiche: Nel controllo qualità e nell'ispezione industriale, la perdita di piccole caratteristiche a causa del sottocampionamento potrebbe impedire il rilevamento di componenti difettosi. Il sovracampionamento può essere utilizzato deliberatamente per lo zoom digitale o per l'elaborazione avanzata.
Quando abbinare Nyquist: sovracampionamento e sottocampionamento
Il campionamento di Nyquist rappresenta l'equilibrio ideale, ma in pratica i sistemi di imaging possono intenzionalmente sovracampionare o sottocampionare a seconda dell'applicazione.
Che cosa è il sottocampionamento
Nel caso di applicazioni in cui la sensibilità è più importante della risoluzione dei più piccoli dettagli, l'utilizzo di una dimensione dei pixel nello spazio oggetto maggiore di quella richiesta dalla legge di Nyquist può portare a notevoli vantaggi nella raccolta della luce. Questo fenomeno è chiamato sottocampionamento.
Ciò sacrifica i dettagli più fini, ma può essere vantaggioso quando:
● La sensibilità è fondamentale: i pixel più grandi raccolgono più luce, migliorando il rapporto segnale/rumore nelle immagini in condizioni di scarsa illuminazione.
● La velocità è importante: un numero inferiore di pixel riduce il tempo di lettura, consentendo un'acquisizione più rapida.
● È richiesta l'efficienza dei dati: nei sistemi con larghezza di banda limitata sono preferibili file di dimensioni ridotte.
Esempio: nell'imaging del calcio o della tensione, i segnali vengono spesso mediati sulle regioni di interesse, quindi il sottocampionamento migliora la raccolta della luce senza compromettere il risultato scientifico.
Che cosa è il sovracampionamento
Al contrario, molte applicazioni per le quali è fondamentale risolvere dettagli fini, o applicazioni che utilizzano metodi di analisi post-acquisizione per recuperare informazioni aggiuntive oltre il limite di diffrazione, richiedono pixel di imaging più piccoli di quelli richiesti da Nyquist, un fenomeno chiamato sovracampionamento.
Sebbene ciò non aumenti la vera risoluzione ottica, può offrire dei vantaggi:
● Consente lo zoom digitale con una minore perdita di qualità.
● Migliora la post-elaborazione (ad esempio, deconvoluzione, denoising, super-risoluzione).
● Riduce l'aliasing visibile quando le immagini vengono successivamente sottocampionate.
Esempio: in microscopia, una fotocamera sCMOS ad alta risoluzione può sovracampionare le strutture cellulari in modo che gli algoritmi computazionali possano estrarre dettagli fini oltre il limite di diffrazione.
Idee sbagliate comuni
1. Più megapixel significano sempre immagini più nitide.
Non è vero. La nitidezza dipende sia dal potere di risoluzione dell'obiettivo sia dalla correttezza del campionamento del sensore.
2. Qualsiasi buon obiettivo funziona bene con qualsiasi sensore ad alta risoluzione.
Una scarsa corrispondenza tra risoluzione dell'obiettivo e pixel pitch limiterà le prestazioni.
3. Il campionamento di Nyquist è rilevante solo nell'elaborazione del segnale, non nell'imaging.
Al contrario, l'imaging digitale è fondamentalmente un processo di campionamento e Nyquist è rilevante in questo caso tanto quanto nell'audio o nelle comunicazioni.
Conclusione
Il campionamento di Nyquist è più di un'astrazione matematica: è il principio che garantisce la sinergia tra risoluzione ottica e digitale. Allineando il potere risolutivo delle lenti con le capacità di campionamento dei sensori, i sistemi di imaging raggiungono la massima nitidezza senza artefatti o sprechi di capacità.
Per i professionisti di settori diversi come la microscopia, l'astronomia, la fotografia e la visione artificiale, comprendere il campionamento di Nyquist è fondamentale per progettare o scegliere sistemi di imaging che forniscano risultati affidabili. In definitiva, la qualità dell'immagine non deriva dall'esagerazione di una specifica, ma dal raggiungimento di un equilibrio.
Domande frequenti
Cosa succede se il campionamento di Nyquist non è soddisfatto in una telecamera?
Quando la frequenza di campionamento scende al di sotto del limite di Nyquist, il sensore non riesce a rappresentare correttamente i dettagli più fini. Questo provoca l'aliasing, che si manifesta sotto forma di bordi frastagliati, effetti moiré o texture false, inesistenti nella scena reale.
In che modo la dimensione dei pixel influisce sul campionamento di Nyquist?
Pixel più piccoli aumentano la frequenza di Nyquist, il che significa che il sensore può teoricamente risolvere dettagli più fini. Ma se l'obiettivo non riesce a fornire quel livello di risoluzione, i pixel extra aggiungono poco valore e potrebbero aumentare il rumore.
Il campionamento Nyquist è diverso per i sensori monocromatici rispetto a quelli a colori?
Sì. In un sensore monocromatico, ogni pixel campiona direttamente la luminanza, quindi la frequenza di Nyquist effettiva corrisponde al pixel pitch. In un sensore a colori con filtro Bayer, ogni canale colore è sottocampionato, quindi la risoluzione effettiva dopo la demosaicizzazione è leggermente inferiore.
Tucsen Photonics Co., Ltd. Tutti i diritti riservati. Nelle citazioni, si prega di citare la fonte:www.tucsen.com
