In imaginibus digitalibus, facile est assumere maiorem resolutionem statim meliores imagines significare. Fabricatores camerarum saepe systemata secundum numerum megapixelorum vendunt, dum fabricatores lentium vim resolutionis et acumen laudant. Attamen, in praxi, qualitas imaginis non solum a specificationibus lentis vel sensoris singillatim pendet, sed etiam a quam bene congruant.
Hic est ubi exemplaris Nyquist in ludum venit. Principium ex processu signorum ortum, criterium Nyquist structuram theoreticam ad accurate capiendas singularitates statuit. In arte imaginandi, efficit ut resolutio optica a lente tradita et resolutio digitalis sensoris camerae concorditer operentur.
Hic articulus rationem Nyquist in contextu imaginum explicat, aequilibrium inter resolutionem opticam et camerae explicat, et normas practicas pro applicationibus a photographica ad imagines scientificas praebet.
Quid est exemplificatio Nyquist?
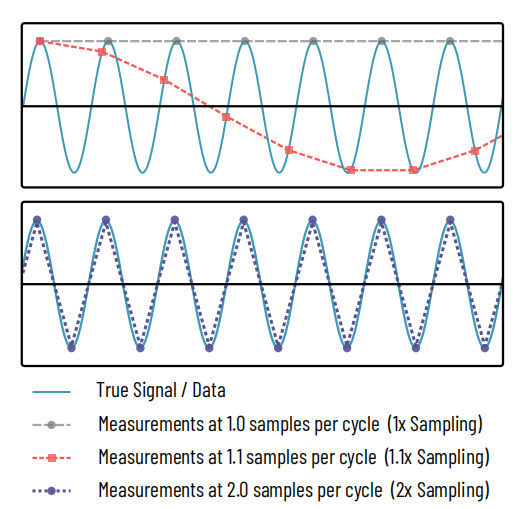
Figura 1: Theorema exemplificationis Nyquistianae
Summum:Signum sinusoidale (caeruleum) in multis punctis mensuratur, vel excerpitur. Linea grisea longa et punctata unam mensuram per cyclum signi sinusoidalis repraesentat, solum cacumina signi captans, veram naturam signi omnino celans. Curva rubra subtiliter punctata 1.1 mensuras per exemplum capit, sinusoidem revelans sed frequentiam eius male repraesentans. Hoc analogum est figurae Moiré.
Imum:Tantum cum duo exempla per cyclum sumuntur (linea purpurea punctata) vera signi natura caperi incipit.
Theorema Nyquist de exemplificatione est principium commune per apparatum signalium in electronicis, apparatu audio, imaginum, aliisque campis. Hoc theorema declarat, ad datam frequentiam in signo reconstruendam, mensuras saltem duplo illius frequentiae fieri debere, quod in Figura 1 demonstratur. In casu resolutionis nostrae opticae, hoc significat magnitudinem pixelis spatii obiecti nostri ad summum dimidiam minimae partis quam capere conamur esse debere, vel, in casu microscopii, dimidiam resolutionis microscopii.
Figura II: Exemplificatio Nyquist cum pixelis quadratis: orientatio interest.
Camera cum reticulo quadratorum pixelorum adhibita, factor exemplificationis bis secundum theorema Nyquist accurate tantum singula capiet quae perfecte cum reticulo pixelorum congruunt. Si structuras ad angulum respectu reticuli pixelorum resolvere conaris, magnitudo pixelorum effectiva maior est, usque ad √2 vicibus maior ad diagonalem. Frequentia exemplificationis igitur bis√2 vicibus maior quam frequentia spatialis desiderata esse debet ad singula ad 45° respectu reticuli pixelorum capienda.
Causa huius perspicua apparet consideratione Figurae 2 (dimidia parte superiori). Finge magnitudinem pixelis ad resolutionem opticam constitutam esse, ita ut cacumina duarum fontium punctualium vicinarum, vel quodlibet detalium quod resolvere conamur, singuli suum pixelum habeant. Quamquam haec deinde separatim deteguntur, nulla indicatio in mensuris resultantibus est ea esse duos cacumina separata – et iterum definitio nostra "resolvendi" non impletur. Pixel intermedius requiritur, qui vallem signi capiat. Hoc perficitur saltem duplicando frequentiam sampling spatialem, id est dimidiando magnitudinem pixelis spatii obiecti.
Resolutio Optica contra Resolutionem Camerae
Ut intellegamus quomodo Nyquist sampling in imaginibus operatur, duo genera resolutionis distinguere debemus:
● Resolutio Optica: A lente determinata, resolutio optica ad facultatem eius ad singula subtiliter repraesentanda refertur. Factores ut qualitas lentis, apertura, et diffractio hunc limitem constituunt. Functio translationis modulationis (MTF) saepe adhibetur ad metiendum quam bene lens contrastum ad diversas frequentias spatiales transmittit.
● Resolutio Camerae: A sensore determinata, resolutio camerae a magnitudine pixelorum, spatio pixelorum, et dimensionibus sensoris totalibus pendet. Spatium pixelorumCamera CMOSFrequentiam Nyquist directe definit, quae maximam detalem quam sensorium capere potest determinat.
Cum haec duo non congruunt, problemata oriuntur. Lens quae vim resolutionis sensoris excedit reapse "perditur", cum sensor non omnia singularia capere possit. Contra, sensor altae resolutionis cum lente inferioris qualitatis coniunctus imagines producit quae non meliorantur quamvis plures megapixels sint.
Quomodo Resolutionem Opticam et Camerae Aequilibrare
Aequilibratio opticae et sensorum significat congruentiam Nyquist sensoris cum frequentia abscissionis opticae lentis.
● Frequentia Nyquist sensoris camerae computatur ut 1 / (2 × spatium pixelis). Haec definit maximam frequentiam spatialem quam sensor sine aliasing capere potest.
● Frequentia abscissionis opticae a proprietatibus lentis et diffractione pendet.
Optimi eventus ad effectum obtinendum, frequentia Nyquist sensoris cum facultate resolutionis lentis congruere debet vel paulo excedere. In praxi, bona regula generalis est curare ut spatium pixelorum (pixel pitch) sit circiter dimidium minimae magnitudinis resolubilis lentis.
Exempli gratia, si lens singula usque ad 4 micrometra resolvere potest, tum sensor cum magnitudinibus pixelorum ~2 micrometrorum systema bene aequabit.
Congruentia Nyquist cum Resolutione Camerae et Provocatio Pixelium Quadratorum
Compromissum cum decrescente magnitudine pixelorum in spatio obiecti est facultas colligendi lucis imminuta. Quare interest aequilibrium inter necessitatem resolutionis et collectionem lucis ponere. Praeterea, maiores magnitudines pixelorum in spatio obiecti solent maiorem campum visionis subiecti imaginandi praebere. In applicationibus quae aliquam necessitatem resolutionis subtilis habent, aequilibrium optimum "regula generalis" sic inveniri dicitur: Magnitudo pixelorum in spatio obiecti, cum per aliquem factorem multiplicatur ad aequationem Nyquist considerandam, resolutioni opticae aequalis esse debet. Haec quantitas resolutio camerae appellatur.
Aequilibratio opticorum et sensorum saepe ad id redit ut resolutio efficax camerae limiti resolutionis opticae lentis respondeat. Systema "Nyquist congruere" dicitur cum:
Resolutio camerae = Resolutio optica
Ubi resolutio camerae datur per:
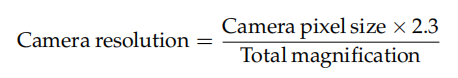
Factor ad rationem Nyquist computandam, qui saepe commendatur, est 2.3, non 2. Huius rei causa haec est.
Elementa camerae (plerumque) quadrata sunt, et in reticulo bidimensionali disposita. Magnitudo elementae, ut in aequatione adversa adhibita definitur, latitudinem elementorum secundum axes huius reticuli repraesentat. Si lineamenta, quae resolvere conamur, ad quemlibet angulum praeter perfectum multiplex 90° respectu huius reticuli iacent, magnitudo elementae effectiva maior erit, usque ad √2 ≈ 1.41 vicibus magnitudinis elementae ad 45°. Hoc in Figura 2 (dimidia parte inferiore) demonstratur.
Factor igitur commendatus secundum criterium Nyquist in omnibus orientationibus esset 2√2 ≈ 2.82. Attamen, propter compromissum antea dictum inter resolutionem et collectionem lucis, valor compromissus 2.3 ut regula generalis commendatur.
Munus Exemplorum Nyquist in Imaginibus
Exemplificatio Nyquist est custos fidelitatis imaginis. Cum frequentia exemplaris infra limitem Nyquist cadit:
● Subexemptio → aliasing efficit: falsa singularia, margines serratos, vel figurae moiré.
● Superexemplar → plura data capit quam optica praebere possunt, quod ad reditus decrescentes ducit: maiores fasciculi et maiores necessitates processus sine meliorationibus visibilibus.
Recta selectio efficit ut imagines et acute sint et realiter fideles. Aequilibrium inter inputum opticum et capturam digitalem praebet, resolutionem inutilem ex una parte vel artefacta fallacia ex altera vitans.
Applicationes Practicae
Nyquist sampling non solum theoria est — applicationes criticas per disciplinas imaginum habet:
● Microscopia:Investigatores sensoria eligere debent quae saltem bis minimam partem a lente obiectiva resolvibilem capiant. Rectam electionem...camera microscopicamagni momenti est, cum magnitudo pixelorum cum resolutione diffractionis limitata obiectivi microscopii congruere debeat. Laboratoria moderna saepe praeferuntCamerae sCMOS, quae aequilibrium sensibilitatis, ambitus dynamici, et structurarum pixellorum subtilium ad imagines biologicas summae perfunctionis praebent.

● Photographia:Coniunctio sensorum multi-megapixelorum cum lentibus quae aeque subtilia singula definire non possunt saepe ad emendationes acutitatis nullius momenti ducit. Photographi periti lentes et cameras librant ne resolutio pereat.
● Photographia:Coniunctio sensorum multi-megapixelorum cum lentibus quae aeque subtilia singula definire non possunt saepe ad emendationes acutitatis nullius momenti ducit. Photographi periti lentes et cameras librant ne resolutio pereat.
● Visio Artificialis &Camerae ScientificaeIn qualitate moderanda et inspectione industriali, si parvae proprietates propter subexemplum desunt, partes vitiosas non deteguntur. Superexemplum consulto ad amplificationem digitalem vel processum amplificatum adhiberi potest.
Quando Nyquist Congruere: Superexemplar et Subexemplar
Exemplificatio Nyquist aequilibrium ideale repraesentat, sed in praxi, systemata imaginandi consulto superexemplare vel subexemplare possunt, pro applicatione.
Quid est subexemplar?
In applicationibus ubi sensus potior est quam minimarum rerum subtilitatum resolutio, usus magnitudinis pixelis in spatio obiecti quae maior est quam postulata Nyquist ad commoda collectionis lucis considerabilia ducere potest. Hoc "undersampling" appellatur.
Hoc subtilitates sacrificat, sed utile esse potest cum:
● Sensibilitas est critica: maiores elementa elementaria plus lucis colligunt, rationem signi ad strepitum in imaginibus sub luce deminuta emendantes.
● Celeritas interest: pauciores elementa elementaria tempus legendi minuunt, acquisitionem celeriorem efficientes.
● Efficientia datorum requiritur: minores magnitudines fasciculorum in systematibus cum latitudine transmissionis limitata praeferuntur.
Exemplum: In imaginibus calcii vel tensionis electricae, signa saepe per regiones interessantes pro rata computantur, ergo subexemptio collectionem lucis emendat sine detrimento exitus scientifici.
Quid est Oversampling?
Contra, multae applicationes quibus subtilitates solvere clavis est, vel applicationes methodos analysis post acquisitionem ad informationes ultra limitem diffractionis recuperandas utentes, minores imagines elementorum quam Nyquist postulat requirunt, quod "oversampling" appellatur.
Quamquam hoc veram resolutionem opticam non auget, tamen commoda afferre potest:
● Zoom digitale cum minore detrimento qualitatis efficit.
● Post-processum emendat (e.g., deconvolutionem, denoising, super-resolutionem).
● Aliasing visibilem minuit cum imagines postea subexemplarentur.
Exemplum: In microscopia, camera sCMOS altae resolutionis structuras cellulares superexemplificet ut algorithmi computationales subtilitates ultra limitem diffractionis extrahere possint.
Falsae opiniones communes
1. Plures megapixeli semper significant imagines acutiores.
Non verum. Acies et a potestate resolutionis lentis et a sensore recte capiendo pendet.
2. Quaevis lens bona bene cum quolibet sensore altae resolutionis operatur.
Mala congruentia inter resolutionem lentis et spatium pixelorum (vel distantiam inter pixellos) efficientiam coercebit.
3. Exemplificatio Nyquist solum in processu signorum pertinet, non in formatione imaginandi.
Contra, imaginatio digitalis fundamentaliter processus exemplificationis est, et Nyquist hic aeque pertinens est ac in audio vel communicationibus.
Conclusio
Exemplificatio Nyquist plus quam abstractio mathematica est — est principium quod efficit ut resolutio optica et digitalis simul operentur. Vim resolutionis lentium cum facultatibus exemplificationis sensorum accommodando, systemata imaginandi maximam claritatem sine artefactis aut capacitate iactura consequuntur.
Peritis in campis tam variis quam microscopia, astronomia, photographia, et visio machinalis, intellegere modum Nyquist sampling est clavis ad designandum vel eligendum systemata imaginandi quae eventus certos praebent. Postremo, qualitas imaginis non ex una specificatione ad extremum impellenda sed ex aequilibrio assequendo oritur.
Quaestiones Frequentes
Quid fit si exemplificatio Nyquist in camera non satisfacit?
Cum frequentia sampling infra limitem Nyquist cadit, sensorium subtilitates recte repraesentare non potest. Hoc ad aliasing perducit, quod apparet ut margines serrati, imagines moiré, vel texturae falsae quae in scena reali non existunt.
Quomodo magnitudo pixelorum (vel pixelorum) sampling Nyquist afficit?
Elementa minore frequentiam Nyquist augent, quod significat sensorem theoretice subtiliora resolvere posse. Sed si lens hunc resolutionis gradum praebere non potest, elementa addita parum valoris addunt et strepitum augere possunt.
Num sampling Nyquist differt pro sensoribus monochromicis et coloratis?
Ita. In sensore monochromico, quisque pixel luminantiam directe exaggerat, ita frequentia Nyquist effectiva cum spatio pixeli congruit. In sensore coloris cum filtro Bayer, quisque canalis coloris subexaggeratur, ita resolutio effectiva post demosaicing paulo inferior est.
Tucsen Photonics Co., Ltd. Omnia iura reservantur. Cum citas, fontem agnosce quaeso:www.tucsen.com

 XXV/IX/IV
XXV/IX/IV