In any measurement system — from wireless communication to digital photography — the signal-to-noise ratio (SNR) is a fundamental benchmark of quality. Whether you are analyzing telescope images, improving microphone recordings, or troubleshooting a wireless link, SNR tells you how much useful information stands out from unwanted background noise.
But calculating SNR correctly is not always straightforward. Depending on the system, additional factors such as dark current, read noise, or pixel binning may need to be considered. This guide walks you through the theory, core formulas, common mistakes, applications, and practical ways to improve SNR, ensuring you can apply it accurately across a wide range of contexts.
What Is Signal-to-Noise Ratio (SNR)?
At its core, signal-to-noise ratio measures the relationship between the strength of a desired signal and the background noise that obscures it.
● Signal = the meaningful information (e.g., a voice in a call, a star in a telescope image).
● Noise = random, unwanted fluctuations that distort or hide the signal (e.g., static, sensor noise, electrical interference).
Mathematically, SNR is defined as:
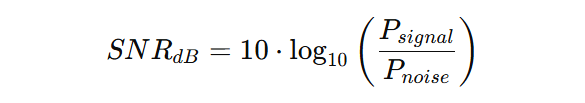
Because these ratios can vary over many orders of magnitude, SNR is usually expressed in decibels (dB):
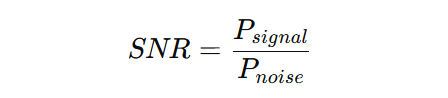
● High SNR (e.g., 40 dB): signal dominates, resulting in clear and reliable information.
● Low SNR (e.g., 5 dB): noise overwhelms the signal, making interpretation difficult.
How to Calculate SNR
Calculation of signal-to-noise ratio can be performed with different levels of precision depending on what noise sources are included. In this section, two forms will be introduced: one that accounts for dark current and one that assumes it can be neglected.
Note: Adding independent noise values requires adding them in quadrature. Each source of noise is squared, summed, and the square root of the total is taken.
Signal-to-noise ratio with dark current
The following is the equation to use in situations where dark current noise is large enough to require inclusion:
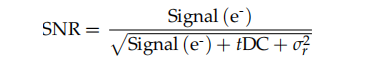
Here is the definition of terms:
Signal (e-): This is the signal of interest in photoelectrons, with the dark current signal subtracted
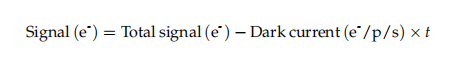
The Total signal (e-) will be the photoelectron count in the pixel of interest – strictly not the pixel value in units of gray levels. The second instance of the Signal (e-), on the bottom of the equation, is the photonshot noise.
Dark current (DC): The dark current value for that pixel.
t: Exposure time in seconds
σr: Read noise in camera mode.
Signal-to-noise ratio for negligible dark current
In the cases of short (< 1 second) exposure times, plus cooled, high-performance cameras, dark current noise will generally be well below read noise, and safely neglected.

Where terms are once again as defined above, with the exception that the dark current signal need not be calculated and subtracted from the signal as it should equal zero.
Limitations of these formulae and missing terms
The formulae opposite will only provide correct answers for CCD and CMOS cameras. EMCCD and intensified devices introduce additional noise sources, so these equations cannot be used. For a more complete signal-to-noise ratio equation that accounts for these and other contributions.
Another noise term that is (or used to be) commonly included in SNR equations is that of the photo-response non-uniformity (PRNU), also sometimes labelled the ‘fixed pattern noise’ (FPN). This represents the unevenness of gain and of signal response across the sensor, which can become dominant at high signals if large enough, reducing SNR.
While early cameras had significant enough PRNU to require its inclusion, most modern scientific cameras have sufficiently low PRNU to make its contribution well below that of photon shot noise, especially after on-board corrections are applied. It is now, therefore, usually neglected in SNR calculations. However, PRNU is still important for some cameras and applications, and is included in the more advanced SNR equation for completeness. This means the equations provided are useful for most CCD/CMOS systems but should not be treated as universally applicable.
Types of Noise in SNR Calculations
Calculating SNR is not just about comparing a signal against a single noise value. In practice, multiple independent noise sources contribute, and understanding them is essential.
Shot Noise
● Origin: statistical arrival of photons or electrons.
● Scales with the square root of the signal.
● Dominant in photon-limited imaging (astronomy, fluorescence microscopy).
Thermal Noise
● It is also called Johnson–Nyquist noise, produced by electron motion in resistors.
● Increases with temperature and bandwidth.
● Important in electronics and wireless communication.
Dark Current Noise
● Random variation in dark current within sensors.
● More significant in long exposures or warm detectors.
● Reduced by cooling the sensor.
Read Noise
● Noise from amplifiers and analog-to-digital conversion.
● Fixed per readout, so critical in low-signal regimes.
Quantization Noise
● Introduced by digitization (rounding to discrete levels).
● Important in low-bit-depth systems (e.g., 8-bit audio).
Environmental/System Noise
● EMI, crosstalk, power supply ripple.
● Can dominate if shielding/grounding is poor.
Understanding which of these is dominant helps in choosing the right formula and mitigation method.
Common mistakes in calculating SNR
It is easy to come across many 'shortcut' methods to estimate a signal-to-noise ratio in imaging. These tend to be either less complex than the equations opposite, allow for easier derivation from an image itself rather than requiring knowledge of camera parameters such as read noise, or both. Unfortunately, it is likely that each one of these methods is incorrect, and will lead to skewed and unhelpful results. It is strongly advised that the equations opposite (or the advanced version should be used in all cases.
Some of the most common false shortcuts include:
1、Comparing signal intensity vs background intensity, in gray levels. This approach attempts to judge camera sensitivity, signal strength or a signal to noise ratio by comparing a peak intensity to a background intensity. This approach is deeply flawed as the influence of camera offset can arbitrarily set the background intensity, gain can arbitrarily set signal intensity, and no contribution of noise either in signal or background is considered.
2、Dividing signal peaks by the standard deviation of an area of background pixels. Or, comparing peak values to the visual noise in the background revealed by a line profile. Assuming that the offset is correctly subtracted from values before division, the most significant danger in this approach is the presence of background light. Any background light will typically dominate the noise in background pixels. Further, the noise in the signal of interest, such as shot noise, is not actually considered at all.
3、Mean signal in pixels of interest vs standard deviation of pixel values: Comparing or observing how much a peak signal changes across neighboring pixels or successive frames is closer to being correct than other shortcut methods, but is unlikely to avoid other influences distorting values, such as a change in the signal that does not derive from noise. This method can also be inaccurate due to low pixel counts in the comparison. Subtraction of offset value must also not be forgotten.
4、Calculating SNR without converting to intensity units of photoelectrons, or without removing the offset: As photon shot noise is typically the largest noise source and relies upon knowledge of the camera’s offset and gain for measurement, it is not possible to avoid calculation back to photoelectrons for SNR calculations.
5、Judging SNR by eye: While in some circumstances judging or comparing SNR by eye can be useful, there are also unexpected pitfalls. Judging SNR in high value pixels can be harder than in lower value or background pixels. More subtle effects can also play a role: For example, different computer monitors can render images with very different contrast. Further, displaying images at different zoom levels in software can significantly influence the visual appearance of noise. This is especially problematic if attempting to compare cameras with different object space pixel sizes. Finally, the presence of background light can void any attempt to judge SNR visually.
Applications of SNR
SNR is a universal metric with wide-ranging applications:
● Audio & Music Recording: Determines clarity, dynamic range, and fidelity of recordings.
● Wireless Communication: SNR relates directly to bit error rates (BER) and data throughput.
● Scientific Imaging: In astronomy, detecting faint stars against background sky glow requires high SNR.
● Medical Equipment: ECG, MRI, and CT scans rely on high SNR to distinguish signals from physiological noise.
● Cameras & Photography: Consumer cameras and scientific CMOS sensors both use SNR to benchmark performance in low light.
Improving SNR
Since SNR is such a critical measure, significant effort goes into improving it. Strategies include:
Hardware Approaches
● Use better sensors with lower dark current.
● Apply shielding and grounding to reduce EMI.
● Cool detectors to suppress thermal noise.
Software Approaches
● Apply digital filters to remove unwanted frequencies.
● Use averaging across multiple frames.
● Employ noise reduction algorithms in imaging or audio processing.
Pixel Binning and Its Effect on SNR
The effect of binning on the signal-to-noise ratio depends upon camera technology and sensor behavior, as the noise performance of binned and unbinned cameras can vary significantly.
CCD cameras can sum adjacent pixels' charge 'on-chip'. The readout noise is only incurred one time, though the dark current signal from each pixel will also be summed.
Most CMOS cameras perform off-chip binning, meaning values are first measured (andread noise introduced), and then summed digitally. The read noise for such summations increases though multiplication by the square root of the number of pixels summed, i.e. by a factor of 2 for 2x2 binning.
As the noise behavior of sensors can be complicated, for quantitative applications it is advisable to measure the offset, gain, and read noise of the camera in binned mode, and use these values for the signal-to-noise ratio equation.
Conclusion
The signal-to-noise ratio (SNR) is one of the most important metrics in science, engineering, and technology. From defining clarity in phone calls to enabling the detection of distant galaxies, SNR underpins the quality of measurement and communication systems. Mastering SNR is not just about memorizing formulas — it’s about understanding assumptions, limitations, and real-world trade-offs. From this perspective, engineers and researchers can make more reliable measurements and design systems that extract meaningful insights even in noisy conditions.
Want to learn more? Take a look at related articles:
Tucsen Photonics Co., Ltd. All rights reserved. When citing, please acknowledge the source: www.tucsen.com


 2025/09/11
2025/09/11