25/09/04Bij digitale beeldverwerking wordt er al snel vanuit gegaan dat een hogere resolutie automatisch betere foto's betekent. Camerafabrikanten brengen systemen vaak op de markt op basis van het aantal megapixels, terwijl lensfabrikanten de nadruk leggen op oplossend vermogen en scherpte. In de praktijk hangt de beeldkwaliteit echter niet alleen af van de specificaties van de lens of sensor afzonderlijk, maar ook van hoe goed ze op elkaar zijn afgestemd.
Hier komt Nyquist-sampling in beeld. Oorspronkelijk een principe uit de signaalverwerking, vormt het Nyquists criterium het theoretische kader voor het nauwkeurig vastleggen van details. Bij beeldvorming zorgt het ervoor dat de optische resolutie van een lens en de digitale resolutie van de sensor van een camera harmonieus samenwerken.
In dit artikel wordt Nyquist-sampling in de context van beeldvorming besproken, wordt de balans tussen optische resolutie en cameraresolutie uitgelegd en worden praktische richtlijnen gegeven voor toepassingen variërend van fotografie tot wetenschappelijke beeldvorming.
Wat is Nyquist-bemonstering?
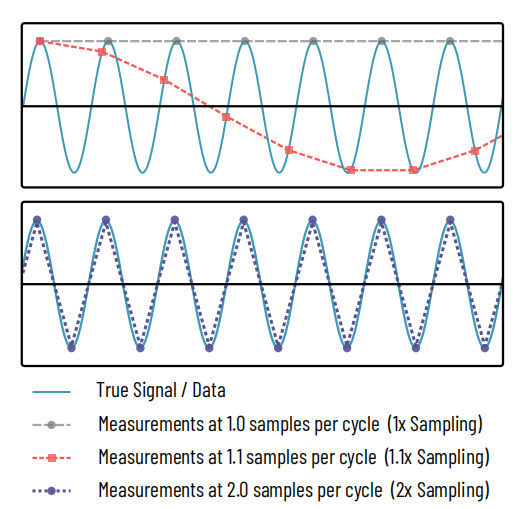
Figuur 1: De Nyquist-steekproefstelling
Bovenkant: Een sinusvormig signaal (cyaan) wordt op meerdere punten gemeten of bemonsterd. De grijze, langgestippelde lijn vertegenwoordigt 1 meting per cyclus van het sinusvormige signaal en registreert alleen signaalpieken, waardoor de ware aard van het signaal volledig verborgen blijft. De rode, fijngestippelde curve registreert 1,1 metingen per monster, wat een sinusoïde onthult, maar de frequentie ervan verkeerd weergeeft. Dit is analoog aan een moirépatroon.
Onderkant:Pas wanneer er per cyclus 2 monsters worden genomen (paarse stippellijn), wordt de ware aard van het signaal vastgelegd.
De Nyquist-bemonsteringsstelling is een principe dat veel voorkomt in signaalverwerking in de elektronica, audioverwerking, beeldvorming en andere vakgebieden. De stelling maakt duidelijk dat om een gegeven frequentie in een signaal te reconstrueren, metingen moeten worden uitgevoerd die minstens twee keer zo hoog zijn als die frequentie, zoals weergegeven in Figuur 1. In het geval van onze optische resolutie betekent dit dat de pixelgrootte in onze objectruimte maximaal de helft mag zijn van het kleinste detail dat we proberen vast te leggen, of, in het geval van een microscoop, de helft van de resolutie van de microscoop.
Figuur 2: Nyquist-bemonstering met vierkante pixels: oriëntatie is van belang
Met een camera met een raster van vierkante pixels zal de 2x-bemonsteringsfactor van de Nyquist-stelling alleen details vastleggen die perfect zijn uitgelijnd met het pixelraster. Bij het bepalen van structuren onder een hoek ten opzichte van het pixelraster is de effectieve pixelgrootte groter, tot wel √2 keer zo groot diagonaal. De bemonsteringsfrequentie moet daarom 2√2 keer de gewenste ruimtelijke frequentie zijn om details vast te leggen onder een hoek van 45 graden ten opzichte van het pixelraster.
De reden hiervoor wordt duidelijk als we Figuur 2 (bovenste helft) bekijken. Stel je voor dat de pixelgrootte is ingesteld op de optische resolutie, waardoor de pieken van twee aangrenzende puntbronnen, of elk detail dat we proberen te onderscheiden, elk een eigen pixel krijgen. Hoewel deze vervolgens afzonderlijk worden gedetecteerd, is er in de resulterende metingen geen enkele aanwijzing dat het twee afzonderlijke pieken zijn – en wederom wordt onze definitie van "oplossen" niet gehaald. Er is een pixel tussenin nodig die een dal van het signaal vastlegt. Dit wordt bereikt door de ruimtelijke bemonsteringsfrequentie ten minste te verdubbelen, oftewel de pixelgrootte van de objectruimte te halveren.
Optische resolutie versus cameraresolutie
Om te begrijpen hoe Nyquist-sampling werkt bij beeldvorming, moeten we onderscheid maken tussen twee soorten resolutie:
● Optische resolutie: Optische resolutie wordt bepaald door de lens en verwijst naar het vermogen om fijne details weer te geven. Factoren zoals lenskwaliteit, diafragma en diffractie bepalen deze grens. De modulatieoverdrachtsfunctie (MTF) wordt vaak gebruikt om te meten hoe goed een lens contrast overbrengt bij verschillende ruimtelijke frequenties.
● Cameraresolutie: De cameraresolutie wordt bepaald door de sensor en is afhankelijk van de pixelgrootte, pixelpitch en de algehele afmetingen van de sensor. De pixelpitch van eenCMOS-cameradefinieert rechtstreeks de Nyquist-frequentie, die bepaalt hoeveel details de sensor maximaal kan vastleggen.
Wanneer deze twee niet op elkaar zijn afgestemd, ontstaan er problemen. Een lens die het oplossend vermogen van de sensor overschrijdt, is effectief "verspild", omdat de sensor niet alle details kan vastleggen. Omgekeerd resulteert een sensor met een hoge resolutie in combinatie met een lens van lage kwaliteit in beelden die ondanks meer megapixels niet verbeteren.
Hoe u optische en cameraresolutie in evenwicht brengt
Het in balans brengen van optica en sensoren betekent het afstemmen van de Nyquist-frequentie van de sensor op de optische afsnijfrequentie van de lens.
● De Nyquist-frequentie van een camerasensor wordt berekend als 1 / (2 × pixelgrootte). Dit definieert de hoogste ruimtelijke frequentie die de sensor kan bemonsteren zonder aliasing.
● De optische afsnijfrequentie is afhankelijk van de lenseigenschappen en diffractie.
Voor de beste resultaten moet de Nyquist-frequentie van de sensor overeenkomen met of iets hoger zijn dan het oplossend vermogen van de lens. In de praktijk is een goede vuistregel om ervoor te zorgen dat de pixelgrootte ongeveer de helft is van de kleinste oplosbare kenmerkgrootte van de lens.
Als een lens bijvoorbeeld details tot 4 micrometer kan waarnemen, dan zal een sensor met pixelgroottes van ~2 micrometer het systeem goed in balans brengen.
Nyquist matchen met cameraresolutie en de uitdaging van vierkante pixels
De afweging bij een afnemende pixelgrootte in de objectruimte is een verminderd vermogen tot lichtopvang. Het is daarom belangrijk om een evenwicht te vinden tussen de behoefte aan resolutie en de behoefte aan lichtopvang. Bovendien zorgen grotere pixelgroottes in de objectruimte doorgaans voor een groter gezichtsveld van het te fotograferen onderwerp. Voor toepassingen die een hoge resolutie vereisen, geldt de volgende vuistregel: de pixelgrootte in de objectruimte, vermenigvuldigd met een factor die rekening houdt met Nyquist, moet gelijk zijn aan de optische resolutie. Deze grootheid wordt cameraresolutie genoemd.
Het in balans brengen van optica en sensoren komt er vaak op neer dat de effectieve bemonsteringsresolutie van de camera overeenkomt met de optische resolutielimiet van de lens. Een systeem wordt "Nyquist-compatibel" genoemd wanneer:
Cameraresolutie = Optische resolutie
Waarbij de cameraresolutie wordt gegeven door:
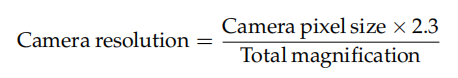
De factor die vaak wordt aanbevolen om rekening te houden met Nyquist is 2,3 en niet 2. De reden hiervoor is als volgt.
Camerapixels zijn (meestal) vierkant en gerangschikt op een 2D-raster. De pixelgrootte zoals gedefinieerd voor gebruik in de vergelijking hiernaast, vertegenwoordigt de breedte van de pixels langs de assen van dit raster. Mochten de objecten die we proberen te onderscheiden zich onder een andere hoek dan een perfect veelvoud van 90° ten opzichte van dit raster bevinden, dan zal de effectieve pixelgrootte groter zijn, tot √2 ≈ 1,41 keer de pixelgrootte bij 45°. Dit wordt weergegeven in Figuur 2 (onderste helft).
De aanbevolen factor volgens het Nyquist-criterium in alle oriëntaties zou daarom 2√2 ≈ 2,82 zijn. Vanwege de eerder genoemde afweging tussen resolutie en lichtopvang wordt echter als vuistregel een compromiswaarde van 2,3 aanbevolen.
De rol van Nyquist-sampling bij beeldvorming
Nyquist-sampling is de poortwachter van de beeldgetrouwheid. Wanneer de samplingfrequentie onder de Nyquist-limiet komt:
● Onderbemonstering→ veroorzaakt aliasing: valse details, gekartelde randen of moirépatronen.
● Oversampling→ legt meer gegevens vast dan de optische technologie kan leveren, wat leidt tot afnemende meeropbrengsten: grotere bestanden en hogere verwerkingsvereisten zonder zichtbare verbeteringen.
Correcte bemonstering zorgt ervoor dat beelden zowel scherp als waarheidsgetrouw zijn. Het zorgt voor de balans tussen optische input en digitale opname, waardoor verspilling van resolutie aan de ene kant en misleidende artefacten aan de andere kant worden voorkomen.
Praktische toepassingen
Nyquist-bemonstering is niet alleen theorie, maar heeft ook cruciale toepassingen in verschillende beeldvormende disciplines:
●Microscopie: Onderzoekers moeten sensoren kiezen die minstens twee keer het kleinste detail dat door de objectieflens kan worden opgelost, kunnen bemonsteren. De juiste keuze makenmicroscopiecamerais cruciaal, omdat de pixelgrootte moet aansluiten op de diffractiegelimiteerde resolutie van het microscoopobjectief. Moderne laboratoria geven vaak de voorkeur aansCMOS-camera's, die een balans bieden tussen gevoeligheid, dynamisch bereik en fijne pixelstructuren voor hoogwaardige biologische beeldvorming.
●AstronomieTelescopen vangen zwakke, verre signalen op. Door sensoren te koppelen aan telescoopoptiek wordt maximale detaillering bereikt zonder artefacten te veroorzaken.
●Fotografie: Het combineren van sensoren met veel megapixels met lenzen die niet even fijne details kunnen vastleggen, resulteert vaak in een verwaarloosbare verbetering van de scherpte. Professionele fotografen balanceren lenzen en camera's om verspilling van resolutie te voorkomen.
●Machinevisie enWetenschappelijke camera'sBij kwaliteitscontrole en industriële inspectie kan het missen van kleine details door ondersampling ertoe leiden dat defecte onderdelen onopgemerkt blijven. Oversampling kan opzettelijk worden gebruikt voor digitale zoom of verbeterde verwerking.
Wanneer je Nyquist moet matchen: oversampling en undersampling
Nyquist-sampling vertegenwoordigt de ideale balans, maar in de praktijk kunnen beeldvormingssystemen opzettelijk over- of ondersamplen, afhankelijk van de toepassing.
Wat is ondersampling?
In toepassingen waarbij gevoeligheid belangrijker is dan het oplossen van de kleinste details, kan het gebruik van een objectruimte met een pixelgrootte die groter is dan de Nyquist-vereisten, leiden tot aanzienlijke voordelen op het gebied van lichtopvang. Dit wordt ondersampling genoemd.
Hierdoor worden fijne details opgeofferd, maar dit kan een voordeel zijn wanneer:
● Gevoeligheid is van cruciaal belang: grotere pixels vangen meer licht op, waardoor de signaal-ruisverhouding bij opnamen bij weinig licht verbetert.
● Snelheid is belangrijk: minder pixels verkorten de uitleestijd, waardoor een snellere acquisitie mogelijk is.
● Gegevensefficiëntie is vereist: kleinere bestandsgroottes zijn beter in systemen met beperkte bandbreedte.
Voorbeeld: Bij calcium- of spanningsbeeldvorming worden signalen vaak gemiddeld over de relevante gebieden. Door onderbemonstering wordt de lichtverzameling verbeterd zonder dat dit ten koste gaat van de wetenschappelijke uitkomst.
Wat is oversampling?
Daarentegen vereisen veel toepassingen waarbij het oplossen van fijne details essentieel is, of toepassingen die post-acquisitie-analysemethoden gebruiken om aanvullende informatie te verkrijgen voorbij de diffractielimiet, kleinere beeldpixels dan Nyquist vereist. Dit wordt oversampling genoemd.
Hoewel dit de werkelijke optische resolutie niet verhoogt, kan het wel voordelen opleveren:
● Maakt digitale zoom mogelijk met minder kwaliteitsverlies.
● Verbetert de nabewerking (bijv. deconvolutie, ruisverwijdering, superresolutie).
● Vermindert zichtbare aliasing wanneer afbeeldingen later worden verkleind.
Voorbeeld: Bij microscopie kan een sCMOS-camera met hoge resolutie cellulaire structuren oversamplen, zodat computeralgoritmen fijne details voorbij de diffractielimiet kunnen extraheren.
Veelvoorkomende misvattingen
1. Meer megapixels betekent altijd scherpere beelden.
Niet waar. Scherpte hangt af van zowel het oplossend vermogen van de lens als van de vraag of de sensor op de juiste manier bemonstert.
2. Elke goede lens werkt goed met elke sensor met een hoge resolutie.
Een slechte match tussen lensresolutie en pixelgrootte beperkt de prestaties.
3. Nyquist-sampling is alleen relevant voor signaalverwerking, niet voor beeldvorming.
Integendeel, digitale beeldvorming is in de basis een bemonsteringsproces, en Nyquist is hierbij net zo relevant als bij audio of communicatie.
Conclusie
Nyquist-sampling is meer dan een wiskundige abstractie – het is het principe dat ervoor zorgt dat optische en digitale resolutie samenwerken. Door het oplossend vermogen van lenzen af te stemmen op de samplingcapaciteit van sensoren, bereiken beeldvormingssystemen maximale helderheid zonder artefacten of verspilling van capaciteit.
Voor professionals in uiteenlopende vakgebieden zoals microscopie, astronomie, fotografie en machine vision is inzicht in Nyquist-sampling essentieel voor het ontwerpen of kiezen van beeldvormingssystemen die betrouwbare resultaten leveren. Uiteindelijk komt beeldkwaliteit niet voort uit het tot het uiterste doorvoeren van één specificatie, maar uit het bereiken van balans.
Veelgestelde vragen
Wat gebeurt er als de camera niet voldoet aan de Nyquist-samplingnorm?
Wanneer de bemonsteringsfrequentie onder de Nyquist-limiet komt, kan de sensor fijne details niet correct weergeven. Dit resulteert in aliasing, wat zich manifesteert als gekartelde randen, moirépatronen of valse texturen die in de echte scène niet voorkomen.
Welke invloed heeft de pixelgrootte op Nyquist-sampling?
Kleinere pixels verhogen de Nyquist-frequentie, wat betekent dat de sensor theoretisch fijnere details kan waarnemen. Maar als de lens die resolutie niet kan leveren, voegen de extra pixels weinig waarde toe en kunnen ze ruis veroorzaken.
Is Nyquist-sampling anders voor monochrome versus kleurensensoren?
Ja. In een monochrome sensor bemonstert elke pixel de luminantie rechtstreeks, waardoor de effectieve Nyquist-frequentie overeenkomt met de pixelgrootte. In een kleurensensor met een Bayer-filter is elk kleurkanaal onderbemonsterd, waardoor de effectieve resolutie na demosaicing iets lager is.
Tucsen Photonics Co., Ltd. Alle rechten voorbehouden. Vermeld bij het citeren de bron:www.tucsen.com
