25/09/04Em imagens digitais, é fácil presumir que maior resolução significa automaticamente fotos melhores. Fabricantes de câmeras frequentemente comercializam sistemas com base na contagem de megapixels, enquanto fabricantes de lentes destacam o poder de resolução e a nitidez. No entanto, na prática, a qualidade da imagem depende não apenas das especificações da lente ou do sensor individualmente, mas também da compatibilidade entre elas.
É aqui que a amostragem de Nyquist entra em ação. Originalmente um princípio do processamento de sinais, o critério de Nyquist define a estrutura teórica para capturar detalhes com precisão. Na geração de imagens, ele garante que a resolução óptica fornecida por uma lente e a resolução digital do sensor de uma câmera funcionem harmoniosamente.
Este artigo analisa a amostragem de Nyquist no contexto da geração de imagens, explica o equilíbrio entre a resolução óptica e a da câmera e fornece diretrizes práticas para aplicações que vão da fotografia à geração de imagens científicas.
O que é amostragem de Nyquist?
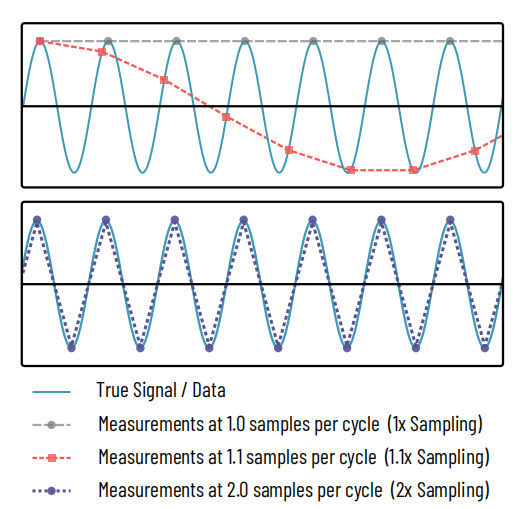
Figura 1: Teorema de amostragem de Nyquist
Principal: Um sinal senoidal (ciano) é medido, ou amostrado, em múltiplos pontos. A linha tracejada longa cinza representa 1 medição por ciclo do sinal senoidal, capturando apenas picos do sinal, ocultando completamente a verdadeira natureza do sinal. A curva tracejada fina vermelha captura 1,1 medição por amostra, revelando uma senoidal, mas deturpando sua frequência. Isso é análogo a um padrão de Moiré.
Fundo:Somente quando 2 amostras são coletadas por ciclo (linha pontilhada roxa) a verdadeira natureza do sinal começa a ser capturada.
O teorema de amostragem de Nyquist é um princípio comum ao processamento de sinais em eletrônica, processamento de áudio, imagens e outras áreas. O teorema deixa claro que, para reconstruir uma determinada frequência em um sinal, as medições devem ser feitas em pelo menos o dobro dessa frequência, conforme mostrado na Figura 1. No caso da nossa resolução óptica, isso significa que o tamanho do pixel do espaço do objeto deve ser, no máximo, metade do menor detalhe que estamos tentando capturar ou, no caso de um microscópio, metade da resolução do microscópio.
Figura 2: Amostragem de Nyquist com pixels quadrados: a orientação é importante
Utilizando uma câmera com uma grade de pixels quadrados, o fator de amostragem 2x do teorema de Nyquist capturará com precisão apenas detalhes perfeitamente alinhados à grade de pixels. Ao tentar resolver estruturas em ângulo com a grade de pixels, o tamanho efetivo do pixel será maior, até √2 vezes maior na diagonal. A taxa de amostragem deve ser, portanto, 2√2 vezes a frequência espacial desejada para capturar detalhes a 45° da grade de pixels.
A razão para isso fica óbvia ao considerar a Figura 2 (metade superior). Imagine que o tamanho do pixel é definido para a resolução óptica, atribuindo aos picos de duas fontes pontuais vizinhas, ou a qualquer detalhe que estejamos tentando resolver, cada um seu próprio pixel. Embora estes sejam detectados separadamente, não há indicação nas medições resultantes de que sejam dois picos separados – e, mais uma vez, nossa definição de "resolução" não é atendida. Um pixel intermediário é necessário, capturando um vale do sinal. Isso é alcançado pelo menos dobrando a taxa de amostragem espacial, ou seja, reduzindo pela metade o tamanho do pixel no espaço do objeto.
Resolução óptica vs. resolução da câmera
Para entender como a amostragem de Nyquist funciona na geração de imagens, precisamos distinguir entre dois tipos de resolução:
● Resolução Óptica: Determinada pela lente, a resolução óptica refere-se à sua capacidade de reproduzir detalhes finos. Fatores como qualidade da lente, abertura e difração definem esse limite. A função de transferência de modulação (MTF) é frequentemente usada para medir a eficiência da transmissão de contraste de uma lente em diferentes frequências espaciais.
● Resolução da Câmera: Determinada pelo sensor, a resolução da câmera depende do tamanho do pixel, do espaçamento entre pixels e das dimensões gerais do sensor. O espaçamento entre pixels de umaCâmera CMOSdefine diretamente sua frequência de Nyquist, que determina o máximo de detalhes que o sensor pode capturar.
Quando esses dois não estão alinhados, surgem problemas. Uma lente que excede o poder de resolução do sensor é efetivamente "desperdiçada", pois o sensor não consegue capturar todos os detalhes. Por outro lado, um sensor de alta resolução combinado com uma lente de baixa qualidade resulta em imagens que não melhoram, apesar de mais megapixels.
Como equilibrar a resolução óptica e da câmera
Balancear a óptica e os sensores significa combinar a frequência de Nyquist do sensor com a frequência de corte óptico da lente.
● A frequência de Nyquist de um sensor de câmera é calculada como 1 / (2 × passo do pixel). Isso define a maior frequência espacial que o sensor pode amostrar sem aliasing.
● A frequência de corte óptico depende das características da lente e da difração.
Para melhores resultados, a frequência de Nyquist do sensor deve estar alinhada ou ligeiramente acima da capacidade de resolução da lente. Na prática, uma boa regra geral é garantir que o pitch do pixel seja aproximadamente metade do menor tamanho de recurso resolvível da lente.
Por exemplo, se uma lente pode resolver detalhes de até 4 micrômetros, então um sensor com tamanhos de pixel de ~2 micrômetros equilibrará bem o sistema.
Combinando Nyquist com a resolução da câmera e o desafio dos pixels quadrados
A desvantagem de reduzir o tamanho do pixel no espaço do objeto é a redução da capacidade de coleta de luz. Portanto, é importante equilibrar a necessidade de resolução e a necessidade de coleta de luz. Além disso, tamanhos maiores de pixel no espaço do objeto tendem a proporcionar um campo de visão maior do objeto fotografado. Para aplicações que exigem alguma resolução fina, diz-se que um equilíbrio ideal, "regra geral", é alcançado da seguinte forma: o tamanho do pixel no espaço do objeto, quando multiplicado por algum fator que leve em conta o Nyquist, deve ser igual à resolução óptica. Essa quantidade é chamada de resolução da câmera.
O balanceamento da óptica e dos sensores muitas vezes se resume a garantir que a resolução efetiva de amostragem da câmera corresponda ao limite de resolução óptica da lente. Diz-se que um sistema "corresponde a Nyquist" quando:
Resolução da câmera = Resolução óptica
Onde a resolução da câmera é dada por:
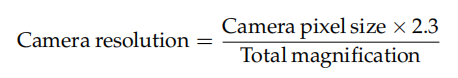
O fator a ser considerado para Nyquist, que geralmente é recomendado, é 2,3, não 2. A razão para isso é a seguinte.
Os pixels da câmera são (tipicamente) quadrados e dispostos em uma grade bidimensional. O tamanho do pixel, conforme definido para uso na equação ao lado, representa a largura dos pixels ao longo dos eixos dessa grade. Caso as características que estamos tentando resolver estejam em qualquer ângulo, exceto um múltiplo perfeito de 90° em relação a essa grade, o tamanho efetivo do pixel será maior, até √2 ≈ 1,41 vezes o tamanho do pixel a 45°. Isso é mostrado na Figura 2 (metade inferior).
O fator recomendado de acordo com o critério de Nyquist em todas as orientações seria, portanto, 2√2 ≈ 2,82. No entanto, devido à compensação mencionada anteriormente entre resolução e coleta de luz, um valor de compromisso de 2,3 é recomendado como regra geral.
O papel da amostragem de Nyquist na obtenção de imagens
A amostragem de Nyquist é a guardiã da fidelidade da imagem. Quando a taxa de amostragem cai abaixo do limite de Nyquist:
● Subamostragem→ causa aliasing: detalhes falsos, bordas irregulares ou padrões moiré.
● Sobreamostragem→ captura mais dados do que a óptica pode fornecer, levando a retornos decrescentes: arquivos maiores e maiores demandas de processamento sem melhorias visíveis.
A amostragem correta garante que as imagens sejam nítidas e fiéis à realidade. Ela proporciona o equilíbrio entre a entrada óptica e a captura digital, evitando desperdício de resolução de um lado ou artefatos enganosos do outro.
Aplicações práticas
A amostragem de Nyquist não é apenas teoria — ela tem aplicações críticas em todas as disciplinas de imagem:
●Microscopia: Os pesquisadores devem escolher sensores que coletem pelo menos o dobro do menor detalhe resolvível pela lente objetiva. Escolher o sensor certocâmera de microscopiaé crítico, pois o tamanho do pixel deve estar alinhado com a resolução limitada pela difração da objetiva do microscópio. Os laboratórios modernos frequentemente preferemcâmeras sCMOS, que fornecem um equilíbrio de sensibilidade, faixa dinâmica e estruturas de pixels finos para imagens biológicas de alto desempenho.
●Astronomia: Telescópios captam sinais tênues e distantes. A combinação de sensores com a óptica do telescópio garante o máximo de detalhes sem introduzir artefatos.
●Fotografia: Combinar sensores de alta resolução com lentes que não conseguem resolver detalhes igualmente precisos geralmente resulta em melhorias insignificantes na nitidez. Fotógrafos profissionais equilibram lentes e câmeras para evitar desperdício de resolução.
●Visão de Máquina eCâmeras Científicas: No controle de qualidade e na inspeção industrial, a ausência de pequenas características devido à subamostragem pode fazer com que peças defeituosas passem despercebidas. A sobreamostragem pode ser usada deliberadamente para zoom digital ou processamento aprimorado.
Quando combinar Nyquist: sobreamostragem e subamostragem
A amostragem de Nyquist representa o equilíbrio ideal, mas, na prática, os sistemas de geração de imagens podem intencionalmente superamostrar ou subamostrar dependendo da aplicação.
O que é subamostragem
No caso de aplicações em que a sensibilidade é mais importante do que a resolução dos mínimos detalhes, usar um tamanho de pixel no espaço do objeto maior do que o exigido por Nyquist pode gerar vantagens consideráveis na coleta de luz. Isso se chama subamostragem.
Isso sacrifica detalhes finos, mas pode ser vantajoso quando:
● A sensibilidade é essencial: pixels maiores coletam mais luz, melhorando a relação sinal-ruído em imagens com pouca luz.
● A velocidade é importante: menos pixels reduzem o tempo de leitura, permitindo uma aquisição mais rápida.
● A eficiência dos dados é necessária: tamanhos de arquivo menores são preferíveis em sistemas com largura de banda limitada.
Exemplo: em imagens de cálcio ou voltagem, os sinais geralmente são calculados em média sobre regiões de interesse, portanto a subamostragem melhora a coleta de luz sem comprometer o resultado científico.
O que é sobreamostragem
Por outro lado, muitas aplicações para as quais a resolução de detalhes finos é fundamental, ou aplicações que usam métodos de análise pós-aquisição para recuperar informações adicionais além do limite de difração, exigem pixels de imagem menores do que os exigidos por Nyquist, o que é chamado de sobreamostragem.
Embora isso não aumente a resolução óptica real, pode oferecer vantagens:
● Permite zoom digital com menos perda de qualidade.
● Melhora o pós-processamento (por exemplo, desconvolução, redução de ruído, super-resolução).
● Reduz o aliasing visível quando as imagens são reduzidas posteriormente.
Exemplo: Na microscopia, uma câmera sCMOS de alta resolução pode sobreamostrar estruturas celulares para que algoritmos computacionais possam extrair detalhes finos além do limite de difração.
Equívocos comuns
1、Mais megapixels sempre significam imagens mais nítidas.
Não é verdade. A nitidez depende tanto do poder de resolução da lente quanto da amostragem adequada do sensor.
2、Qualquer boa lente funciona bem com qualquer sensor de alta resolução.
Uma correspondência ruim entre a resolução da lente e o pitch dos pixels limitará o desempenho.
3. A amostragem de Nyquist é relevante apenas no processamento de sinais, não em imagens.
Pelo contrário, a imagem digital é fundamentalmente um processo de amostragem, e Nyquist é tão relevante aqui quanto em áudio ou comunicações.
Conclusão
A amostragem de Nyquist é mais do que uma abstração matemática — é o princípio que garante que as resoluções óptica e digital funcionem em conjunto. Ao alinhar o poder de resolução das lentes com as capacidades de amostragem dos sensores, os sistemas de imagem alcançam a máxima clareza sem artefatos ou desperdício de capacidade.
Para profissionais de áreas tão diversas como microscopia, astronomia, fotografia e visão computacional, compreender a amostragem de Nyquist é fundamental para projetar ou escolher sistemas de imagem que ofereçam resultados confiáveis. Em última análise, a qualidade da imagem não advém da aplicação de uma especificação ao extremo, mas sim da busca pelo equilíbrio.
Perguntas frequentes
O que acontece se a amostragem de Nyquist não for satisfeita em uma câmera?
Quando a taxa de amostragem cai abaixo do limite de Nyquist, o sensor não consegue representar detalhes finos corretamente. Isso resulta em aliasing, que aparece como bordas irregulares, padrões moiré ou texturas falsas que não existem na cena real.
Como o tamanho do pixel afeta a amostragem de Nyquist?
Pixels menores aumentam a frequência de Nyquist, o que significa que o sensor pode, teoricamente, resolver detalhes mais finos. Mas se a lente não consegue fornecer esse nível de resolução, os pixels extras agregam pouco valor e podem aumentar o ruído.
A amostragem de Nyquist é diferente para sensores monocromáticos e coloridos?
Sim. Em um sensor monocromático, cada pixel amostra a luminância diretamente, de modo que a frequência de Nyquist efetiva corresponde ao pitch do pixel. Em um sensor de cor com filtro Bayer, cada canal de cor é subamostrado, de modo que a resolução efetiva após o demosaicing é ligeiramente menor.
Tucsen Photonics Co., Ltd. Todos os direitos reservados. Ao citar, por favor, mencione a fonte:www.tucsen.com
