25/09/04Inom digital bildbehandling är det lätt att anta att högre upplösning automatiskt innebär bättre bilder. Kameratillverkare marknadsför ofta system baserade på megapixelantal, medan objektivtillverkare betonar upplösningsförmåga och skärpa. I praktiken beror dock bildkvaliteten inte bara på specifikationerna för objektivet eller sensorn individuellt, utan också på hur väl de är matchade.
Det är här Nyquist-sampling kommer in i bilden. Ursprungligen en princip från signalbehandling, sätter Nyquists kriterium den teoretiska ramen för att fånga detaljer korrekt. Inom bildbehandling säkerställer det att den optiska upplösningen som levereras av ett objektiv och den digitala upplösningen hos en kameras sensor fungerar harmoniskt tillsammans.
Den här artikeln analyserar Nyquist-sampling i samband med avbildning, förklarar balansen mellan optisk och kameraupplösning och ger praktiska riktlinjer för tillämpningar som sträcker sig från fotografi till vetenskaplig avbildning.
Vad är Nyquist-provtagning?
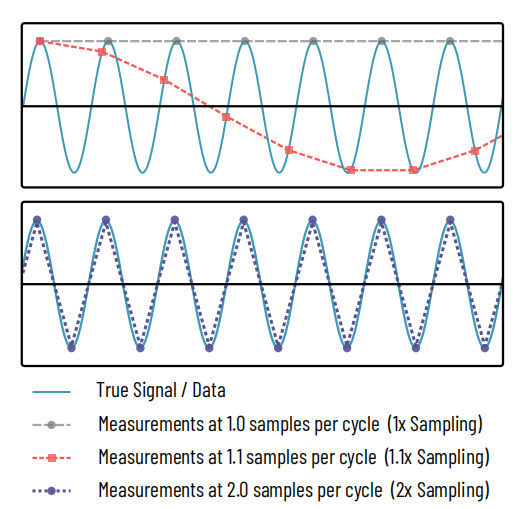
Figur 1: Nyquists samplingsteorem
BästaEn sinusformad signal (cyan) mäts, eller samplas, vid flera punkter. Den grå långstreckade linjen representerar 1 mätning per cykel av sinussignalen och fångar endast signaltoppar, vilket helt döljer signalens sanna natur. Den röda, fint streckade kurvan fångar 1,1 mätningar per sampel, vilket avslöjar en sinusformad signal men felaktigt representerar dess frekvens. Detta är analogt med ett moirémönster.
BottenFörst när 2 prover tas per cykel (lila streckad linje) börjar signalens sanna natur fångas upp.
Nyquists samplingsteorem är en princip som är vanlig inom signalbehandling inom elektronik, ljudbehandling, bildbehandling och andra områden. Satsen klargör att för att rekonstruera en given frekvens i en signal måste mätningar göras minst dubbelt så höga som frekvensen, vilket visas i figur 1. När det gäller vår optiska upplösning innebär detta att vår objektrymds pixelstorlek får vara högst hälften av den minsta detalj vi försöker fånga, eller, när det gäller ett mikroskop, hälften av mikroskopets upplösning.
Figur 2: Nyquist-sampling med kvadratiska pixlar: orientering spelar roll
Med en kamera med ett rutnät av kvadratiska pixlar kommer Nyquists sats 2x samplingsfaktor endast att exakt fånga detaljer som är perfekt justerade i pixelrutnätet. Om man försöker upplösa strukturer i en vinkel mot pixelrutnätet är den effektiva pixelstorleken större, upp till √2 gånger större vid diagonalen. Samplingsfrekvensen måste därför vara 2√2 gånger den önskade rumsfrekvensen för att fånga detaljer i 45° mot pixelrutnätet.
Anledningen till detta blir uppenbar genom att betrakta figur 2 (övre halvan). Tänk dig att pixelstorleken är inställd på den optiska upplösningen, vilket ger topparna för två angränsande punktkällor, eller någon detalj vi försöker upplösa, var sin egen pixel. Även om dessa sedan detekteras separat, finns det ingen indikation i de resulterande mätningarna på att de är två separata toppar – och återigen uppfylls inte vår definition av "upplösning". En pixel däremellan behövs, som fångar ett dalvärde av signalen. Detta uppnås genom att åtminstone fördubbla den rumsliga samplingsfrekvensen, dvs. halvera objektets pixelstorlek.
Optisk upplösning kontra kameraupplösning
För att förstå hur Nyquist-sampling fungerar vid avbildning måste vi skilja mellan två typer av upplösning:
● Optisk upplösning: Bestäms av linsen och avser dess förmåga att återge fina detaljer. Faktorer som linsens kvalitet, bländare och diffraktion sätter denna gräns. Modulationsöverföringsfunktionen (MTF) används ofta för att mäta hur väl en lins överför kontrast vid olika rumsliga frekvenser.
● Kameraupplösning: Kameraupplösningen bestäms av sensorn och beror på pixelstorlek, pixeltäthet och sensorns totala dimensioner. Pixeltätheten för enCMOS-kameradefinierar direkt dess Nyquist-frekvens, vilket bestämmer den maximala detaljnivån som sensorn kan fånga.
När dessa två inte är i linje uppstår problem. En lins som överskrider sensorns upplösningsförmåga är i praktiken "bortkastad", eftersom sensorn inte kan fånga alla detaljer. Omvänt resulterar en högupplöst sensor i kombination med en lins av låg kvalitet i bilder som inte förbättras trots fler megapixlar.
Hur man balanserar optisk och kameraupplösning
Att balansera optik och sensorer innebär att matcha sensorns Nyquist-frekvens med linsens optiska gränsfrekvens.
● Nyquistfrekvensen för en kamerasensor beräknas som 1 / (2 × pixelavstånd). Detta definierar den högsta rumsliga frekvensen som sensorn kan sampla utan aliasing.
● Den optiska gränsfrekvensen beror på linsens egenskaper och diffraktion.
För bästa resultat bör sensorns Nyquistfrekvens vara i linje med eller något överstiga linsens upplösningsförmåga. I praktiken är en bra tumregel att se till att pixelstorleken är ungefär hälften av linsens minsta upplösningsbara funktionsstorlek.
Om till exempel ett objektiv kan upplösa detaljer ner till 4 mikrometer, kommer en sensor med pixelstorlekar på ~2 mikrometer att balansera systemet väl.
Att matcha Nyquist med kameraupplösning och utmaningen med fyrkantiga pixlar
Avvägningen med minskande pixelstorlek i objektutrymmet är minskad ljusinsamlingsförmåga. Det är därför viktigt att balansera behovet av upplösning och ljusinsamling. Dessutom tenderar större pixelstorlekar i objektutrymmet att ge ett större synfält för det avbildade motivet. För tillämpningar som har ett visst behov av fin upplösning sägs en optimal balans "tumregel" vara följande: Pixelstorleken i objektutrymmet, multiplicerad med någon faktor för att ta hänsyn till Nyquist, bör vara lika med den optiska upplösningen. Denna kvantitet kallas kameraupplösning.
Att balansera optik och sensorer handlar ofta om att säkerställa att kamerans effektiva samplingsupplösning matchar objektivets optiska upplösningsgräns. Ett system sägs "matcha Nyquist" när:
Kameraupplösning = Optisk upplösning
Där kamerans upplösning ges av:
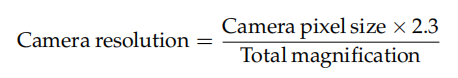
Den faktor som ofta rekommenderas för att ta hänsyn till Nyquist är 2,3, inte 2. Anledningen till detta är följande.
Kamerapixlar är (vanligtvis) kvadratiska och arrangerade i ett 2D-rutnät. Pixelstorleken som definieras för användning i ekvationen mittemot representerar bredden på pixlarna längs axlarna i detta rutnät. Om de funktioner vi försöker lösa upp ligger i någon vinkel förutom en perfekt multipel av 90° i förhållande till detta rutnät, kommer den effektiva pixelstorleken att vara större, upp till √2 ≈ 1,41 gånger pixelstorleken vid 45°. Detta visas i figur 2 (nedre halvan).
Den rekommenderade faktorn enligt Nyquistkriteriet i alla orienteringar skulle därför vara 2√2 ≈ 2,82. På grund av den tidigare nämnda avvägningen mellan upplösning och ljusinsamling rekommenderas dock ett kompromissvärde på 2,3 som tumregel.
Nyquist-samplingens roll i avbildning
Nyquist-sampling är grindvakten för bildåtergivning. När samplingsfrekvensen faller under Nyquist-gränsen:
● Undersampling→ orsakar aliasing: falska detaljer, ojämna kanter eller moirémönster.
● Översampling→ fångar in mer data än optiken kan leverera, vilket leder till minskande avkastning: större filer och högre bearbetningskrav utan synliga förbättringar.
Korrekt sampling säkerställer att bilderna är både skarpa och verklighetstrogna. Det ger balansen mellan optisk ingång och digital inspelning, vilket undviker slöseri med upplösning på ena sidan eller vilseledande artefakter på den andra.
Praktiska tillämpningar
Nyquist-provtagning är inte bara teori – den har viktiga tillämpningar inom olika bilddiscipliner:
●MikroskopiForskare måste välja sensorer som samlar in minst dubbelt så mycket detaljer som objektivlinsen kan upplösa. Att välja rättmikroskopikameraär avgörande, eftersom pixelstorleken måste anpassas till mikroskopets diffraktionsbegränsade upplösning. Moderna laboratorier föredrar oftasCMOS-kameror, vilket ger en balans mellan känslighet, dynamiskt omfång och fina pixelstrukturer för högpresterande biologisk avbildning.
●AstronomiTeleskop fångar svaga, avlägsna signaler. Att matcha sensorer med teleskopoptik säkerställer maximal detaljrikedom utan att introducera artefakter.
●FotografiAtt para ihop sensorer med höga megapixlar med objektiv som inte kan lösa lika fina detaljer resulterar ofta i försumbara förbättringar av skärpan. Professionella fotografer balanserar objektiv och kameror för att undvika slöseri med upplösning.
●Maskinseende ochVetenskapliga kamerorVid kvalitetskontroll och industriell inspektion kan saknade små funktioner på grund av undersampling innebära att defekta delar inte upptäcks. Översampling kan användas avsiktligt för digital zoom eller förbättrad bearbetning.
När man ska matcha Nyquist: Översampling och undersampling
Nyquist-sampling representerar den ideala balansen, men i praktiken kan avbildningssystem avsiktligt översampla eller undersampla beroende på tillämpningen.
Vad är undersampling
I tillämpningar där känslighet är viktigare än att lösa de minsta detaljerna, kan användning av en pixelstorlek i objektutrymmet som är större än vad Nyquist kräver leda till avsevärda fördelar med ljusinsamling. Detta kallas undersampling.
Detta offrar fina detaljer, men kan vara fördelaktigt när:
● Känslighet är avgörande: större pixlar samlar in mer ljus, vilket förbättrar signal-brusförhållandet vid bilder i svagt ljus.
● Hastighet spelar roll: färre pixlar minskar avläsningstiden, vilket möjliggör snabbare bildtagning.
● Dataeffektivitet krävs: mindre filstorlekar är att föredra i system med begränsad bandbredd.
Exempel: Vid kalcium- eller spänningsavbildning medelvärdesbildas signaler ofta över intressanta områden, så undersampling förbättrar ljusinsamlingen utan att kompromissa med det vetenskapliga resultatet.
Vad är översampling
Omvänt kräver många tillämpningar där det är viktigt att lösa fina detaljer, eller tillämpningar som använder metoder för efterförvärv för att återställa ytterligare information bortom diffraktionsgränsen, mindre bildpixlar än Nyquist kräver, vilket kallas översampling.
Även om detta inte ökar den verkliga optiska upplösningen, kan det ge fördelar:
● Möjliggör digital zoom med mindre kvalitetsförlust.
● Förbättrar efterbehandling (t.ex. dekonvolution, brusreducering, superupplösning).
● Minskar synliga aliasing-effekter när bilder nedsamplas senare.
Exempel: Inom mikroskopi kan en högupplöst sCMOS-kamera översampla cellulära strukturer så att beräkningsalgoritmer kan extrahera fina detaljer bortom diffraktionsgränsen.
Vanliga missuppfattningar
1. Fler megapixlar betyder alltid skarpare bilder.
Inte sant. Skärpan beror både på objektivets upplösningsförmåga och om sensorn samplar korrekt.
2. Alla bra objektiv fungerar bra med alla högupplösta sensorer.
En dålig överensstämmelse mellan objektivets upplösning och pixeltäthet kommer att begränsa prestandan.
3. Nyquist-sampling är endast relevant vid signalbehandling, inte vid avbildning.
Tvärtom är digital bildbehandling i grunden en samplingsprocess, och Nyquist är lika relevant här som inom ljud eller kommunikation.
Slutsats
Nyquist-sampling är mer än en matematisk abstraktion – det är principen som säkerställer att optisk och digital upplösning fungerar tillsammans. Genom att anpassa linsernas upplösningsförmåga till sensorernas samplingskapacitet uppnår bildsystem maximal skärpa utan artefakter eller slöseri med kapacitet.
För yrkesverksamma inom så skilda områden som mikroskopi, astronomi, fotografi och maskinseende är förståelse för Nyquist-provtagning nyckeln till att utforma eller välja avbildningssystem som ger tillförlitliga resultat. I slutändan kommer bildkvalitet inte från att pressa en specifikation till det yttersta utan från att uppnå balans.
Vanliga frågor
Vad händer om Nyquist-samplingen inte är uppfylld i en kamera?
När samplingsfrekvensen faller under Nyquist-gränsen kan sensorn inte återge fina detaljer korrekt. Detta resulterar i aliasing, vilket uppträder som ojämna kanter, moirémönster eller falska texturer som inte finns i den verkliga scenen.
Hur påverkar pixelstorleken Nyquist-sampling?
Mindre pixlar ökar Nyquistfrekvensen, vilket innebär att sensorn teoretiskt sett kan lösa upp finare detaljer. Men om objektivet inte kan leverera den upplösningsnivån, tillför de extra pixlarna lite värde och kan öka bruset.
Är Nyquist-sampling annorlunda för monokroma jämfört med färgsensorer?
Ja. I en monokrom sensor samplar varje pixel luminans direkt, så den effektiva Nyquist-frekvensen matchar pixelhöjden. I en färgsensor med ett Bayer-filter undersamplas varje färgkanal, så den effektiva upplösningen efter demosaicing är något lägre.
Tucsen Photonics Co., Ltd. Med ensamrätt. Vänligen ange källan vid citering:www.tucsen.com
